Method for Determining the Representative Mean Radiant Temperature for Heating and Cooling Control Application

Sung-Jin Kwon; Dong-Seok Lee

doi:10.22696/jkiaebs.20240015

Preview

Research Article

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems. 30 June 2024. 165-174
https://doi.org/10.22696/jkiaebs.20240015

Method for Determining the Representative Mean Radiant Temperature for Heating and Cooling Control Application

냉난방 제어 적용을 위한 평균복사온도 대푯값 산정방법

Sung-Jin Kwon¹

Dong-Seok Lee²^*

권 성진¹

이 동석²^*

¹Master’s Course Student, Department of Architecture, Keimyung University, Daegu, Korea

²Assistant Professor, Department of Architectural Engineering, Keimyung University, Daegu, Korea

¹계명대학교 대학원 건축학과 석사과정

²계명대학교 건축공학전공 조교수, 공학박사

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

The mean radiant temperature (MRT) is a critical element affecting occupant thermal comfort in indoor spaces. However, because the spatial distribution of MRT values varies, it is difficult to provide MRT information to the building heating and cooling control system. This study provides a brief review of the existing methods for determining the representative MRT value in a single zone and suggests a method to derive its reasonable value. First, three existing methods of determining the representative MRT were reviewed, and their limitations were analyzed. Then, a new method was proposed to address these limitations. Finally, an experimental study was conducted to compare the representative MRT values obtained from both the existing and proposed methods under two different shading control conditions. The results of this study highlight the significance of measuring and applying MRT in real building operations.

Keywords

Mean Radiant Temperature

Longwave and Shortwave Radiation

Thermal environment

키워드

평균복사온도

장단파복사

온열환경

MAIN

서 론
평균복사온도 대푯값 산정방법 고찰
기존 평균복사온도 대푯값 산정 방법
동일온도법(Method A)
단일지점측정법(Method B)
면적가중법(Method C)
평균복사온도 대푯값 산정방법 제안
실험 및 분석
실험개요
평균복사온도 대푯값 산정방법 분석
Discussion
결론

서 론

건물에서는 재실자를 위한 쾌적한 온열환경을 조성하기 위해, 다양한 자연형 및 설비형 시스템을 제어한다. 이중 많은 종류의 시스템들이 장파와 단파 복사를 직접 제어하는 열전달 방식을 가지고 있다. 실내외 차양장치, 천정 및 바닥 복사 냉난방 등의 시스템들이 그 예이다. 재실자가 느끼는 종합적인 온열환경을 평가하기 위해서는 4가지 물리적 인자(공기온도, 평균복사온도, 기류속도, 습도)와 2가지 개인적 인자(착의량, 활동량)를 고려할 수 있다(ISO 7730, 2005). 물리적 인자 중에서, 평균복사온도(mean radiant temperature, MRT)는 인체가 느끼는 온열감에 약 절반정도 수준의 영향을 준다고 보고된 바 있다(Guo et al., 2020). 또한, 이는 앞서 기술된 장파와 단파 복사 제어 시스템들이 주는 온열환경 영향을 가장 빠르게 직접적으로 나타내는 인자가 된다. 그러므로 평균복사온도의 인체 온열환경 영향 정도와 건물에서 사용되는 냉난방 제어 시스템들의 열전달 방식을 고려하였을 때, 평균복사온도를 고려한 종합적인 온열환경 평가와 이를 기반으로한 냉난방 제어는 중요하다고 볼 수 있다.

단일 존(zone)에서 온열환경 평가 결과는 하나의 값으로 냉난방 제어 시스템에 전달된다. 그러므로 공기온도( $t_{a}$ )와 같이 평균복사온도를 냉난방 제어에 적용하기 위해서는 대상 존의 복사 환경을 종합하여 표현할 수 있는 하나의 대푯값이 필요하다. 하지만 평균복사온도는 공간내 위치에 따른 편차가 크기 때문에(Guo et al., 2020), 이에 대한 대푯값 산정이 어려워 진다. 이에 기존 연구에서는 주로 공간 내 특정 지점을 선정하여 평가해왔다(Sung et al., 2023; Qahtan, 2024). 따라서 정확한 대푯값 산정방법이 필요하다.

본 연구에서는 기존 연구에서 다루어진 평균복사온도 대푯값 산정 방법들에 관하여 검토하고 기존 방법들이 가진 한계점을 보완하기 위한 평균복사온도 대푯값 산정 방법을 제안하였다. 실측 실험을 통해서 실내 복사 온도의 분포를 확인하고, 기존 방법들과 본 연구에서 제안된 방법을 비교 분석하였다.

평균복사온도 대푯값 산정방법 고찰

기존 평균복사온도 대푯값 산정 방법

Ciabattoni et al. (2015)은 퍼지 컨트롤러(모호하거나 불확실한 정보를 처리하여 시스템의 제어 결정을 내리는 데 사용되는 논리 기반 시스템)를 통한 실내 열쾌적 제어와 PMV (predicted mean vote)최적화에 대한 연구를 진행하면서 평균복사온도를 공기온도와 동일하다고 가정하였다. Sung et al. (2023)은 실내공간 내외주부의 하절기 평균복사온도 가상센싱 모델을 개발하는 연구에서 측정 센서를 외주부와 실의 중앙에 설치하였다. Cheong et al. (2014)의 연구에서는 실내 표면의 평균 온도 값을 각 표면 넓이에 따라 가중 평균하는 방법을 사용하여 평균복사온도를 도출하였다. 기존 연구에서 사용되고 있는 평균복사온도 대푯값 산정방법을 나타내면 다음과 같다(See Figure 1). 본 연구에서는 방법의 명칭 구분을 위해, 이를 Method A, B, C로 각각 정의하였다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-03/N0280180301/images/Figure_KIAEBS_18_3_01_F1.jpg

Figure 1.

Concept of the presentative MRT values

ㆍMethod A: 평균복사온도와 공기온도가 동일하다고 가정하는 방법

(Ciabattoni et al., 2015; Walikewitz et al., 2015; Deng and Chen, 2018)

ㆍMethod B.: 실의 중앙(또는 외주부) 내 1개 지점을 선정하여 측정하는 방법

(Sung et al., 2023; Qahtan, 2024)

ㆍMethod C: 실내 표면별 평균온도 값을 각 표면 넓이에 따라 가중 평균하는 방법

(Cheong et al., 2014; Wang et al., 2019; Lou et al., 2020)

동일온도법(Method A)

Method A는 평균복사온도와 공기온도가 동일하다고 가정하는 방법이다. 장단파를 모두 고려하지 않는 방법으로, 실내 존재하는 공기온도 센서를 이용해서 평균복사온도를 도출하는 방법이다. 식 (1)은 평균복사온도와 공기온도가 동일하다고 하는 평균복사온도( ${\bar{t}}_{r, air}$ ) 계산방법이다.

(1)

{\bar{t}}_{r, air} (t) = t_{a} (t)

여기서, $t_{a}$ 는 공기온도[℃]이다. 공기온도센서를 통해 측정되는 대류 열전달 방식은 복사온도 측정센서가 갖는 열전달 방식과 다르다. 그러므로, 공기온도 센서를 통해서는 복사열환경에 대한 정보를 공기온도를 통해서는 복사열교환 정보를 제공할 수 없다. 주변으로부터 장파복사나 태양 일사로부터 전달되는 단파복사와 관련된 열전달의 영향을 고려하지 못한다.

단일지점측정법(Method B)

Method B는 실의 중앙(또는 외주부)내 1개 지점을 선정하여 측정하는 방법이다. 장단파를 모두 고려하는 방법으로, 측정은 흑구온도계로 직접 측정하거나, 열화상 카메라로 형상계수(angle factor)와 표면온도의 관계를 이용해서 측정할 수 있다. 이 방법은 주로 흑구온도계가 적용된다. 식 (2)는 흑구온도계를 기반으로 하는 평균복사온도 ( ${\bar{t}}_{r, pt}$ )계산 방법을 이용하는 방법이다(ISO 7726, 1998).

(2)

{\bar{t}}_{r, pt} (t) = {[(t_{g} (t) + 273.15)^{4} + \frac{1.1 \times 10^{8} \times v_{a}^{0.6} (t)}{ε_{g} \times D^{0.4}} (t_{g} (t) - t_{a} (t))]}^{\frac{1}{4}} - 273.15

여기서, $t_{g}$ 는 흑구온도[℃], $v_{a}$ 는 기류속도[m/s]이다. $ε_{g}$ 는 흑구의 방사율[-], $D$ 는 흑구의 지름[m]이다. 이 방법은 재실자의 자세에 따른 형상계수를 고려하지 못한다. 그러나 흑구로 입사되는 장파와 단파복사를 모두 고려할 수 있는 방법이다.

면적가중법(Method C)

Method C는 실내 표면별 평균온도 값을 각 표면 넓이에 따라 가중 평균하는 방법이다. 실내 표면온도 측정을 위해 접촉식 또는 비접촉식 표면온도 측정 센서를 이용한다. 식 (3)는 실내 표면온도와 면적 가중평균 방법을 이용하여 평균복사온도( ${\bar{t}}_{r, area}$ )를 산정하는 식이다.

(3)

{\bar{t}}_{r, area} (t) = \frac{\sum_{j = 1}^{n} t_{s_{j}} (t) a_{j}}{\sum_{j = 1}^{n} a_{j}}

여기서, $t_{s_{j}}$ 는 j번째 실내표면의 온도[℃], $a_{j}$ 는 j번째 실내 표면이다. 이 방법은 전체 면적에 누락되는 데이터가 없이 모든 데이터를 사용하고 모든 표면의 면적을 고려하기 때문에 실의 대한 대표적인 하나의 값을 도출할 수 있는 방법이 될 수 있다. 그러나 이 방법은 표면 온도에 따른 장파 복사만을 고려하는 방법이다. 다양한 차양 시스템이 제어될 때 달라지는 일사의 유입량 변화(단파 복사)는 고려하지 못한다.

기존 방법들은 장단파 복사 영향에 대한 고려 유무가 다른 것으로 검토되었다. Method A는 장단파를 고려하지 않고 Method B는 장단파를 모두 고려하는 방법이다. Mehtod C는 장파만 고려하는 방법이다.

또한, 측정 위치에 따라서도 각 측정방법들을 통해 도출되는 평균복사온도 값이 다를 것으로 예상되었다. Method A는 공기온도 값을 사용하므로 대류가 충분한 공간의 경우 측정 위치에 따른 편차가 상대적으로 작다. Method B는 하나의 지점에 센서를 설치하므로 설치된 위치가 창으로부터 떨어진 거리, 대상 공간의 향(동, 서, 남, 북) 등이 평균복사온도 값에 매우 큰 영향을 준다. 즉, 센서가 설치된 위치에 따라 평균복사온도 값의 편차가 매우 커질 수 있다. Method C는 전체적인 공간에서 복사에 대한 영향을 다 고려를 하지만 단파 복사는 고려되지 않는다. Table 1은 기존에 사용되던 평균복사온도 도출방법 3가지와 새롭게 제안하는 방법의 특징을 비교한 것이다.

Table 1.

Comparison of MRT characteristics according to measurement methods

Method	Consideration of		Advantages	Disadvantages	Reference
Method	SW	LW	Advantages	Disadvantages	Reference
Air temperature method	-	-	∙No additional sensor installation	∙No consideration of radiation	Ciabattoni et al., 2015
Point measurement method	O	O	∙Consideration of both LW and SW radiation	∙No consideration of spatial MRT distributions	Sung et al., 2023
Area weighting method	-	O	∙A single value representing the entire space	∙Without consideration of shortwave radiation	Cheong et al., 2014

평균복사온도는 위치에 따라서 장단파 복사의 편차가 커진다. Lee and Jo (2021)의 연구에서는 겨울철 실내 평균복사온도는 위치에 따라 15℃ 편차가 난다고 보고하였다. 위 연구 결과를 고려하였을 때 센서의 설치 위치에 따른 편차와 장단파 복사의 고려 유무가 대상 공간이 실제와 가까운 복사 운영 환경을 평가하는데 중요한 요소라고 할 수 있다. 기존의 방법들을 보완하여 장단파 복사의 영향과 측정 위치에 따른 편차를 고려할 수 있는 방법이 필요하다.

평균복사온도 대푯값 산정방법 제안

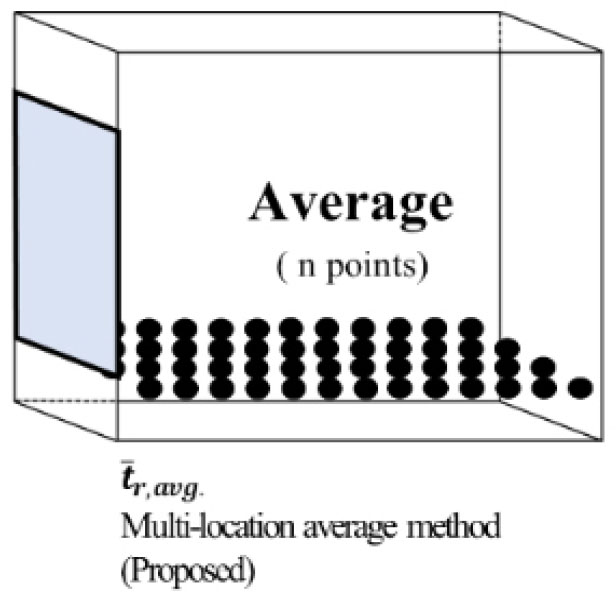
평균복사온도는 다중 지점 위치에 따라서 다양한 분포를 가질 수 있다. Lee and Jo (2022)의 연구에서는 열화상 카메라를 이용해서 단일 존(zone) 내에서도 측정 위치에 따라서 평균복사온도가 다양하게 분포됨을 확인하였다. 그러므로 해당 공간의 대표성을 갖는 평균복사온도를 냉난방 시스템 설비제어에 입력해주기 위해서는 공간내에 분포된 평균복사온도 값을 평균하는 방법이 현재로서는 가장 정확한 방법이라고 할 수 있다. 기존 연구자들이 진행한 열화상 카메라 측정 방법과 접촉식 온도 센서를 이용하는 방법은 형상계수(angle factor)를 이용해서 다양한 위치에서의 평균복사온도를 계산을 통해서 도출하기 때문에 다양한 지점에서의 평균복사온도를 빠르게 도출할 수 있다는 장점이 있다. 따라서 본 연구는 존(zone)의 n개에 해당하는 다중 존의 위치를 균등분할하는 위치로 선정하여 이를 평균화하는 방법을 제안하였다. 제안된 방법( ${\bar{t}}_{r, avg}$ )을 도식화하여 나타내면 Figure 2와 같다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-03/N0280180301/images/Figure_KIAEBS_18_3_01_F2.jpg

Figure 2.

The proposed method for deriving representative values of MRT

n개의 위치에서의 평균복사온도 측정값과 이를 평균하는 방법을 식으로 나타내면 식 (4)와 같다.

(4)

{\bar{t}}_{r, avg .} (t) = \frac{\sum_{i = 1}^{n} {\bar{t}}_{r, pt} (i, t)}{n}

여기서, n은 측정 지점수, i는 재실자 위치, t는 시간이다. 실내 표면온도는 IR camera를 이용하여 측정하였으며, 실내 입사 일사량은 수평면 전일사계와 직산 분리모델을 이용하여 측정하였다(Lee and Jo, 2021). 평균복사온도를 계산하기 위한 식은 식 (5)와 같이 계산된다.

(5)

\begin{aligned} {\bar{t}}_{r}^{l, k} (i, t) \\ = {(\sum_{i} T_{S_{j}}^{4} (j, t) F_{i - j} (i, j) + \frac{α^{k}}{σ ε_{P}} \sum_{j} I_{dif}^{' ⊢} (j^{'}, t) F_{i - j^{'}} (i, j^{'}) + \frac{α^{k}}{σ ε_{P}} f_{proj} I_{DN}^{'} (i, t))}^{0.25} - 273.15 \end{aligned}

여기서, $T_{S_{j}} (j, t)$ 는 시간 t에 따른 실내 표면 j의 표면 절대온도이다. $I'_{dif}^{⊢} (j', t)$ 는 시간 t에 따른 유리 표면 $j'$ 를 통과해 입사되는 확산일사량이고, $I'_{DN} (i, t)$ 는 유리를 통과하여 시간 t에 따른 재실자 위치 i로 입사되는 직달일사량이다. $F_{i - j} (i, j)$ 는 재실자의 위치 i와 모든 실내 표면 j사이의 형상계수이다. $f_{proj}$ 는 인체 투영 면적에 대한 비율이다. $α^{k}$ 는 단파복사 흡수율로 0.57로 설정하였고, σ는 Stefan-Boltzmann 상수로 $5.67 \times 10^{- 8} [{Wm}^{- 2} K^{- 4}]$ 값을 갖는다. $ε_{P}$ 는 재실자의 방사율로 0.97로 설정했다(Lee and Jo, 2022).

실험 및 분석

실험개요

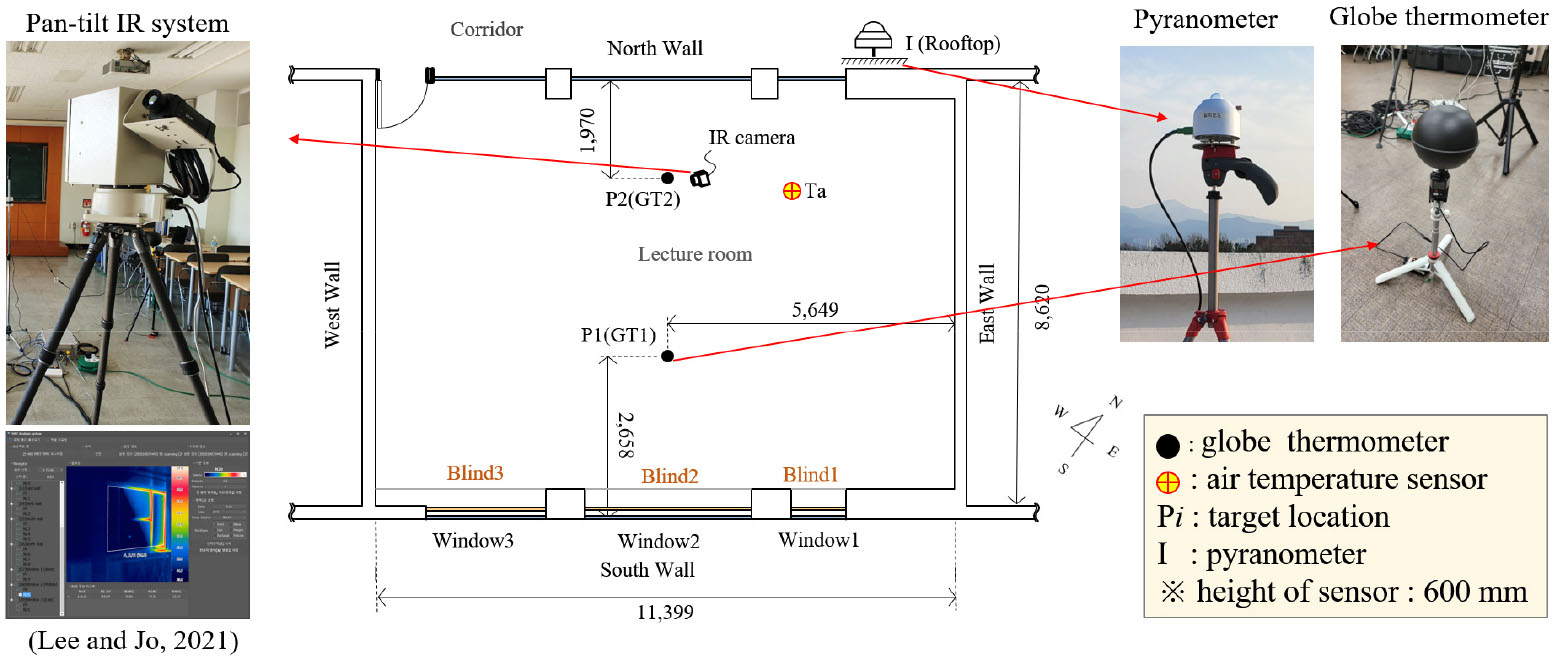
대상 공간은 대구 소재 대학교 강의실을 선정하였다. 남쪽에 3개의 창문과 롤 블라인드가 설치되어 있고, 북쪽으로는 3개의 유리벽이 있고, 복도가 위치한다(Figure 3). 온도와 일사량이 유사한 두개의 날짜에 롤 블라인드의 설정에 따라, Case 1 (Shade OFF)과 Case 2 (Shade ON)로 구분하였다.

실험 측정 기간(23/02/21, 23/02/25) 동안 실내 온도(21일 평균 15.7℃, 25일 평균 15.6℃)와 일사(21일 평균 200.5 W/m², 25일 평균 203.6 W/m²는 거의 유사한 기후를 보였다. 재실자의 위치 선정은 실내 공간적인 분포를 확인하기 위해 외주부(P1), 내주부(P2)를 각각 선정하였다. 측정 위치에 따른 평균복사온도의 차이와 분포 특성을 확인하기 위해, 기존 연구에서 개발된 Pan-tilt IR scanning system (Lee and Jo, 2021)을 이용한 방법을 적용하였다. 평균복사온도 예측 방법은 기존의 연구 결과를 그대로 적용하였다. 측정위치는 실내 공간을 균등 분할하는 2500개의 지점으로 선정하였다. 공기온도센서는 일사의 영향을 받지 않는 중간 위치로 선정하였다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-03/N0280180301/images/Figure_KIAEBS_18_3_01_F3.jpg

Figure 3.

Plan of the experimental set

측정에 사용된 장비 현황은 Table 2와 같다. ${\bar{t}}_{r, air}$ 는 Thermo-hygrometer를 사용하였고, ${\bar{t}}_{r, pt}$ 는 Pan-tilt IR scanning system와 GT를 사용하여 측정하였다. ${\bar{t}}_{r, area}$ 는 Pan-tilt IR scanning system, ${\bar{t}}_{r, avg}$ 는 Pan-tilt IR scanning system와 Pyranometer를 사용하여 측정하였다.

Table 2.

Specification of the measuring devices

Device name	Specifications
Pan-tilt IR scanning system	Model / Accuarcy	FLIR A310 / ± 2℃
Globe thermometer	Model / Accuarcy	Testo Globe probe / ± 1℃
Pyranometer	Model / Accuarcy	MS-40 / ± 12W/m²
Thermo-hygrometer	Model / Accuarcy	Testo 174H / (T) ± 0.5℃, (RH) ± 3%

평균복사온도 대푯값 산정방법 분석

평균복사온도 계산을 위해서는 실시간 측정되는 표면 영역별 평균표면온도 값과 각 재실자 위치에서의 표면 별 형상계수(angle factor) 계산이 필요하다. 이때 형상계수는 1회성으로 계산된 후에는 더 이상 계산이 불필요한 과정이다. 형상계수 계산은 입체각(solid angle) 계산방법을 적용하였다(Eriksson et al., 1990). 형상계수는 앉아있는 재실자의 상태를 가정하여 바닥으로부터 높이 600 mm로 설정하여 계산하였다. 이 후 표면온도 모니터링을 통해 재실자 위치 별 실시간 평균복사온도 값을 측정하였다.

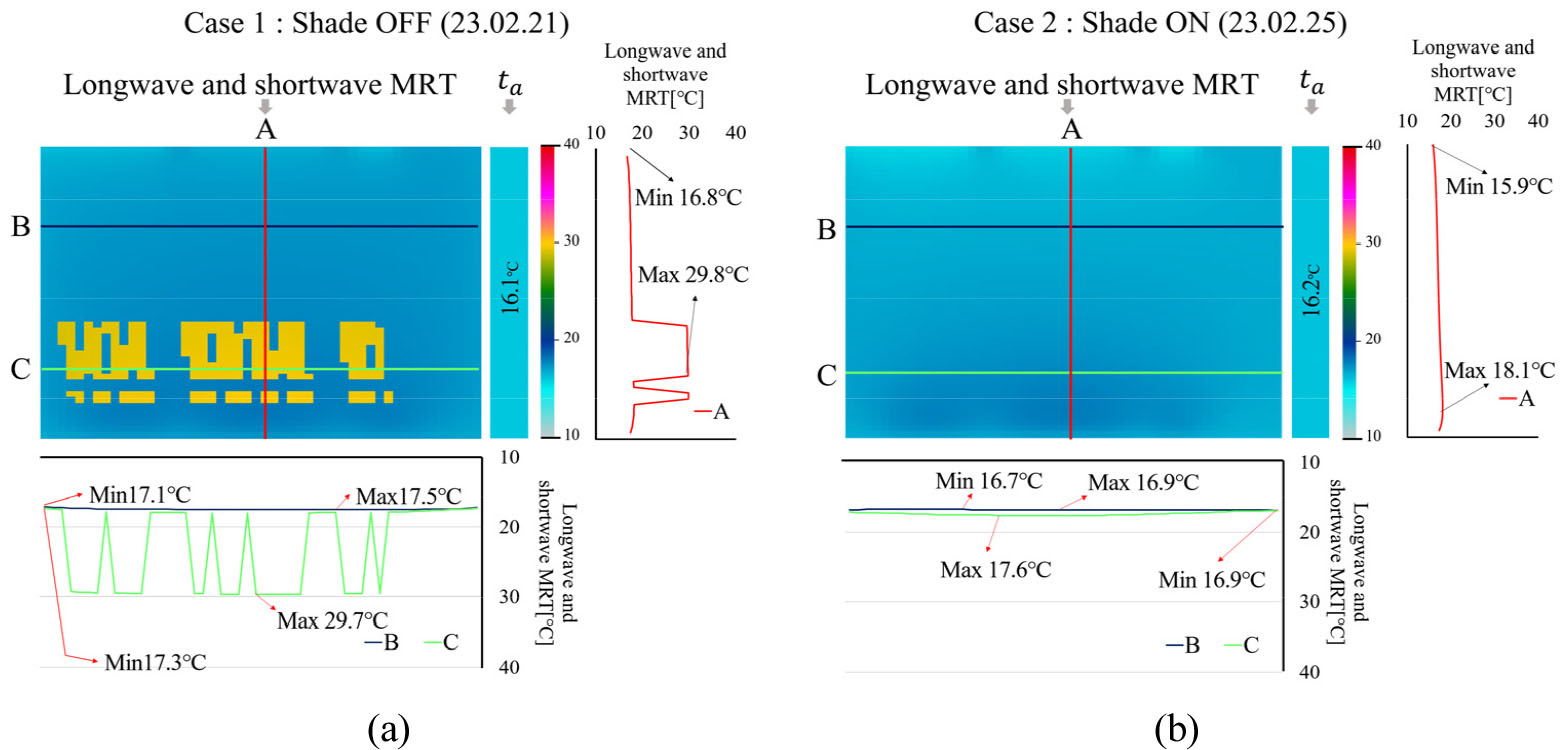
측정 위치에 따른 평균복사온도( ${\bar{t}}_{r} (i, t)$ )의 차이와 분포 특성을 확인하기 위하여, 열화상 카메라를 이용하는 기존 연구 결과물을 적용하였다(Lee and Jo, 2022). Figure 4은 차양 제어에 따른 재실자의 위치와 시간에 따라서 ${\bar{t}}_{r} (i, t)$ 값의 차이와 분포 특성에 대해서 나타낸다. 차양제어 방식이 다른 날, 같은 시간(10시 5분)에 측정된 $t_{a}$ 값과 LW & SW ${\bar{t}}_{r}$ 값을 비교한 결과, 위치에 따라 두 값의 차이가 크게 나타나는 것(e.g.: 13.8℃)을 확인하였다. ${\bar{t}}_{r} (i, t)$ 또한 위치(a-B, a-C)에 따라 차이가 크게(e.g.: 13.5℃) 나타나는 것으로 확인되었다. 평균복사온도는 측정 위치에 따라 매우 큰 차이를 가진다. 따라서 어느 한 위치에서 측정된 값을 대푯값으로 산정하기에는 한계가 있다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-03/N0280180301/images/Figure_KIAEBS_18_3_01_F4.jpg

Figure 4.

Measurement results of MRT distribution (a) Case 1 10:05 (b) Case 2 10:05

Table 3.

Measured MRT values for different cases and times according to the applied measurement methods (Case 1: Shade OFF, Case 2: Shade ON)

Cases	Applied methods		Representative MRT values measured at time (hh:mm)
			09:05	12:05	15:05	18:05
Case 1 (2/21)	${\bar{t}}_{r, air}$		15.2	17.0	16.4	15.6
	${\bar{t}}_{r} (p, t)$	Center	16.4	18.0	17.1	16.3
		P1 / P2	16.2/16.2	17.9/17.6	16.8/16.8	16.2/16.3
	${\bar{t}}_{r, area}$		15.8	17.5	16.5	15.8
	${\bar{t}}_{r, avg}$		19.2	18.4	17.0	16.2

Case 2 (2/25)	${\bar{t}}_{r, air}$		15.6	16.7	16.0	15.3
	${\bar{t}}_{r} (i\p, t)$	Center	16.6	17.4	16.5	16.0
		P1 / P2	17.0 / 16.2	17.9 / 17.0	16.6 / 16.3	16.0 / 15.9
	${\bar{t}}_{r, area}$		16.6	17.7	16.4	15.8
	${\bar{t}}_{r, avg}$		16.4	17.3	16.5	16.0

Table 3은 시간별로 차양 제어에 따른 평균복사온도 대푯값 산정 방법 도출결과이다. 9시 5분부터 18시 5분까지 3시간 간격으로 4번의 각각 다른 시간의 산정 방법별로 계산하여 비교하였다. Case 1은 Shade OFF인 상태로 제안된 방식( ${\bar{t}}_{r, avg}$ )은 일사의 영향 규모에 따른 편차가 다른 방법들의 차이가 커지는 것을 확인할 수 있었다. $t_{a}$ 값은 가장 낮은 온도가 측정되었다. ${\bar{t}}_{r} (p, t)$ 값은 일사의 영향이 없는 시간에서는 제안된 방법과 유사한 값을 보였으나 일사 영향이 있는 시간대에서는 제안된 방법과 큰 차이를 보였다. ${\bar{t}}_{r, area}$ 값은 공기온도와 가장 유사한 경향을 보였다. Case 2는 Shade ON인 상태로 대부분 유사한 경향을 보였으나, 공기온도와 평균복사온도는 다르게 나타나는 것을 확인할 수 있다.

Discussion

본 연구에서는 초기 연구 단계에서의 대푯값 산정방법을 다루었으며 측정 지점의 개수와 위치에 대한 상세한 분석내용은 다루지 않았다. 기존 연구 및 표준 등에서 측정 포인트 개수 및 위치에 대한 내용은 다루어진 바가 없으나, 극장이나 돔경기장 등과 같이 단일 공간이 매우 큰 경우가 아닌 일반적인 중소규모 공간에서는 2500개의 측정 개소로 충분할 것으로 판단된다. 그러나 공간의 다양성을 고려하여 제안된 2500개 측정 개수의 적절성과 계산 시간 최소화 방법에 대한 향후 연구가 필요할 것으로 판단된다. 측정 개수가 작아질 경우 측정 위치에 따른 평균복사온도 값의 오차가 발생할 수 있으므로 이에 대한 고려도 필요하다. 본 연구에서는 2500개로 균등분할하는 측정 위치의 개수가 해당 공간의 평균복사온도 분포를 충분히 반영할 수 있을 것으로 판단하여 이를 적용한 평균복사온도 대푯값 산정방법을 제안하였다.

공간 평균복사온도 분포를 반영한 대푯값 산정방법( ${\bar{t}}_{r, avg}$ )은 장파와 단파 복사를 종합적으로 고려한 냉난방제어를 가능하게 할 것으로 판단된다. Figure 4와 같이 차양이 제어될 경우 차양 제어 효과를 분석할 수 있으며, 복사 냉난방 시스템의 경우 제안된 방법을 통해 장파 제어의 효과도 분석할 수 있을 것으로 판단된다. 본 연구의 결과는 OT 및 PMV 등과 같은 공기온도와 복사온도를 모두 고려한 냉난방 제어의 중요성을 보고한다. 향후 연구에서는 다양한 시스템 제어에 대한 제안된 산정방법의 적용성에 대하여 검토할 예정이다.

결론

평균복사온도는 실내 공간에서 거주자의 온열쾌적성에 중요한 요소다. 그러나 평균복사온도는 공간 내 위치에 따라 편차가 크기 때문에, 건물의 다양한 설비형 시스템 제어에 정보를 제공하기는 어렵다. 따라서 온열환경 평가에 있어 정확한 대푯값 산정이 필요하다. 기존 연구에서 사용되고 있는 평균복사온도 대푯값 산정방법들은 장파 및 단파복사의 고려 유무와 측정 위치에 따라 차이를 보인다. 따라서 본 연구에서는 기존의 방법들을 보완하여 장단파 복사의 영향과 측정 위치에 따른 편차를 고려한 대푯값 산정 방법들을 제안하였다.

제안된 방법은 실내 불균등하게 분포하는 평균복사온도의 평균값을 대푯값으로 산정하는 방법이다. 온도와 일사량이 유사한 겨울철 두 개의 날짜에 차양의 ON/OFF에 따라 구분하여 실험을 진행하였다. 실험을 통해 평균복사온도는 공기온도보다 낮 동안 높은 수준을 유지하는 경향을 보였다. 이는, 공기온도만을 기준으로 평가한다면 실제 재실자가 느끼는 온열감보다 더 낮은 수준을 나타낼 수 있으므로, 난방 제어에 있어서 에너지 소비가 증가되는 결과를 가져올 수 있다는 것을 의미한다. 그러나 본 연구의 결과는 측정 개소를 2500개로 선정하여 진행하였기 때문에 측정 개소의 개수에 대한 비교 분석과 측정 개소가 많아질수록 계산 시간을 최소화하는 방안에 대한 추가적인 연구도 필요하다. 본 연구의 후속 연구로, 측정 개소에 따른 평균복사온도 대푯값 케이스 비교와 다양한 평균복사온도 대푯값 산정방법 비교 연구를 진행할 예정이다.

Acknowledgements

이 논문은 2023년도 한국연구재단의 지원을 받아 수행된 연구임 과제번호(NRF-2022R1C1C2007250).

References

Cheong, C.-H., Hwang, S.-H., Park, B.-Y. (2014). Analysis on Indoor Thermal Comfort of Buildings in Campus during Intermediate Season. Journal of the Regional Association of Architectural Institute of Korea, 16(4).

Deng, Z., Chen, Q. (2018). Artificial Neural Network Models Using Thermal Sensations and Occupants' Behavior for Predicting Thermal Comfort'. Energy and Buildings, 174, 587-602.

10.1016/j.enbuild.2018.06.060

Eriksson, F. (1990). On the Measure of Solid Angle. Math. Assoc. Am., 63(3), 184-187.

10.1080/0025570X.1990.11977515

Guo, H., Aviva, D., Loyola, M., Teitelbaum, E., Houchois, N., Meggers, F. (2020). On the understanding of the mean radiant temperature within both the indoor and outdoor environment, a critical review. Renewable and Sustainable Energy Reviews, 117, 109207.

10.1016/j.rser.2019.06.014

Lee, D.-S., Jo, J.H. (2021). Pan-Tilt Ir Scanning Method for the Remote Measurement of Mean Radiant Temperatures at Multi-Location in Buildings. Remote Sensing, 13(11).

10.3390/rs13112158

Lee, D.-S., Jo, J.-H. (2022). Application of IR camera and pyranometer for estimation of longwave and shortwave mean radiant temperatures at multiple locations. Build. Environ., 207, 108423.

10.1016/j.buildenv.2021.108423

Lou, R., Hallinan, K.P., Huang, K., Reissman, T. (2020). Smart Wifi Thermostat-Enabled Thermal Comfort Control in Residences'. Sustainability (Switzerland), 12(5), 1-15.

10.3390/su12051919

Qahtan, A.M. (2024). Aesthetic and Thermal Suitability of Highly Glazed Spaces with Interior Roller Blinds in Najran University Buildings, Saudi Arabia. Sustainability, 16(5).

10.3390/su16052030

Sung, S.-H., Yun, W.-S., Ryu, W.-T., Seo, H.-C., Hong, W.-H. (2023). Development of Mean Radiant Temperature Virtual Sensor for Core and Perimeter Zones during the Summer Using Random Forest. Journal of the Architectural Institute of Korea, 39(3), 171-177.

Walikewitz, N., Janicke, B., Langner, M., Meier, F., Endlicher, W. (2015). The Difference between the Mean Radiant Temperature and the Air Temperature within Indoor Environments: A Case Study during Summer Conditions. Building and Environment, 84, 151-161.

10.1016/j.buildenv.2014.11.004

Wang, D., Chen, G., Song, C., Liu, Y., He, W., Zeng, T., Liu, J. (2019). Experimental Study on Coupling Effect of Indoor Air Temperature and Radiant Temperature on Human Thermal Comfort in Non-Uniform Thermal Environment. Building and Environment, 165, 106387.

10.1016/j.buildenv.2019.106387

Ciabattoni, L., Cimini, G., Ferracuti, F., Grisostomi, M., Ippoliti, G., Matteo, P. (2015). Indoor Thermal Comfort Control through Fuzzy Logic PMV Optimization. Proceedings of the International Joint Conference on Neural Networks, 12-17.

10.1109/IJCNN.2015.7280698

ISO 7726. (1998). Ergonomics of the thermal environment - Instruments for measuring physical quantities.

ISO 7730. (2005). Moderate thermal environments: determination of the PMV and PPD Indices and Specification of the conditions of Thermal Comfort.

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems ISSN:1976-6483(Print) 2586-0666(Online) 한국건축친환경설비학회논문집

Preview

Method for Determining the Representative Mean Radiant Temperature for Heating and Cooling Control Application

ABSTRACT

MAIN

Figure 1.

Concept of the presentative MRT values

(1)

(2)

(3)

Table 1.

Comparison of MRT characteristics according to measurement methods

Figure 2.

The proposed method for deriving representative values of MRT

(4)

(5)

Figure 3.

Plan of the experimental set

Table 2.

Specification of the measuring devices

Figure 4.

Measurement results of MRT distribution (a) Case 1 10:05 (b) Case 2 10:05

Table 3.

Measured MRT values for different cases and times according to the applied measurement methods (Case 1: Shade OFF, Case 2: Shade ON)

Acknowledgements

References