서 론
격자 품질에 대한 이론적 배경
격자 품질 예측 모델 개발 방법
격자 품질 예측을 위한 형상 특성 지표 선정
데이터셋 구축을 위한 CFD 모델 설계 방법
다중선형회귀분석을 통한 격자 품질 예측 모델 구축 방법
격자 품질 예측 모델 도출 결과
대상 시설 및 형상 특성 지표 산정
대상 시설별 격자 설계 및 품질 결과
형상 특성 지표별 격자 품질 영향 분석
다중회귀분석을 통한 격자 품질 예측 모델 도출
결 론
서 론
전산유체역학(Computational Fluid Dynamics, CFD)을 포함한 수치 해석 기법에서는 분석 대상 공간을 유한개의 격자로 분할하는 과정이 중요하다. 분할된 격자를 기반으로 유체의 흐름 특성을 표현한 Navier-Stokes 방정식을 수치해석하기 때문에, 격자의 품질이 전체 해석 결과에 중요한 영향을 미친다. 설계된 격자의 품질이 좋지 않을 경우 이산화 오차나 반올림 오차, 절단 오차 등 근사해의 오차가 증가하며 시뮬레이션의 수렴성을 저하시키는 주요 원인이 된다(Tu et al., 2018). 이는 CFD 시뮬레이션의 결과 정확도가 떨어지는 주요한 원인 중 하나이다. 따라서 정확한 해석 결과를 얻기 위해서는 높은 품질의 격자 모델을 설계하는 것이 필요하다.
격자의 품질은 형상과 격자 조건의 영향을 동시에 받기 때문에 고품질의 격자 모델 설계를 위해서는 형상 최적화, 격자 최적화 과정을 함께 고려해야 한다. 건축물은 수많은 창문, 기둥, 돌출부, 곡면 등을 포함하고 있으며, 이러한 복잡한 형상으로 인하여 격자의 품질이 저하된다(Park et al., 2020). 격자 품질을 개선하기 위한 형상 최적화 방법으로 형상 단순화 방법이 주로 이용된다(Ricci et al., 2017). 그러나 형상 단순화와 같이 분석 대상의 복잡한 형상을 처리하는 과정은 많은 시행착오와 작업 시간이 요구된다(Ali et al., 2019). 형상 최적화와 별개로 격자 최적화는 격자 독립성 검증을 통해 수행된다. 격자 독립성 검정은 다수의 격자 크기에 대하여 결과의 오차가 발생하지 않으면서 가장 적은 수의 격자 설계가 가능한 조건을 찾는 과정을 수행한다. 따라서 다수의 격자 크기에 대한 모델 설계와 시뮬레이션이 수반되어 많은 작업량과 시간이 요구된다. 이와 같이 격자의 품질을 향상시키기 위해서는 반복적인 작업이 요구되기 때문에, CFD 모델 설계의 작업량 및 소요시간이 증가하며 나아가 CFD 분석의 생산성이 저하된다.
격자 품질을 개선에 많은 시행착오와 시간이 소요되는 주요 원인은 격자 품질에 대한 예측이 불가능하여 모든 방법에 대하여 형상 모델 및 격자 모델 설계가 요구되기 때문이다. 실제 설계 과정 없이 격자 품질을 예측이 가능하면 형상 최적화와 격자 최적화 과정에서 발생하는 시행착오를 줄이고 작업시간을 절감할 수 있다. 또한 다양한 최적화 방법에 대한 격자 품질 평가를 신속하게 하여 CFD 분석의 생산성 향상이 가능하다. 격자 품질의 중요성으로 인하여 이와 관련한 국내 및 국외 연구는 활발하게 이루어지고 있으나 격자 품질 예측과 관련된 연구는 전무하다. 대부분의 기존 연구는 격자 품질을 개선하기 위한 격자 생성 및 처리 방법(Makem et al., 2014; Gargallo-Peiró et al., 2014; Ma and Zhao, 2015), 격자 품질을 평가하는 방법(Chen et al., 2020; Xu et al., 2020)에 국한되어 있다. 한편, CFD 이외 분야에서는 분석 대상의 형상을 이용하여 3차원 모델의 visual quality를 회귀 모델, 기계 학습 등을 활용하여 예측하는 연구가 일부 진행되고 있다(Abouelaziz et al., 2017; Chetouani, 2017). 그러나 격자 품질과 visual quality 그리고 각 지표에 영향을 주는 형상 특성이 상이하여 CFD 분야에 적합한 예측 모델 개발이 필요하다.
따라서 본 연구에서는 분석 대상의 형상 특성 중 격자 품질에 영향을 주는 인자를 선정하고 다중선형회귀분석을 통해 격자 품질을 예측하는 모델을 개발하였다. 예측 모델 개발을 위하여 우선적으로 격자 품질에 대한 이론적 고찰을 수행하였으며, 격자 품질에 주요한 영향을 주는 형상 특성 지표를 선정하였다. 다중선형회귀분석을 위한 데이터 셋 구축을 위하여 개방형 CFD 분석 도구인 OpenFOAM을 대상으로 육면체 격자계에 대한 케이스 스터디를 수행하였다. 케이스 스터디 결과를 바탕으로 형상 특성 지표를 활용한 격자 품질 예측 모델을 개발하였다
격자 품질에 대한 이론적 배경
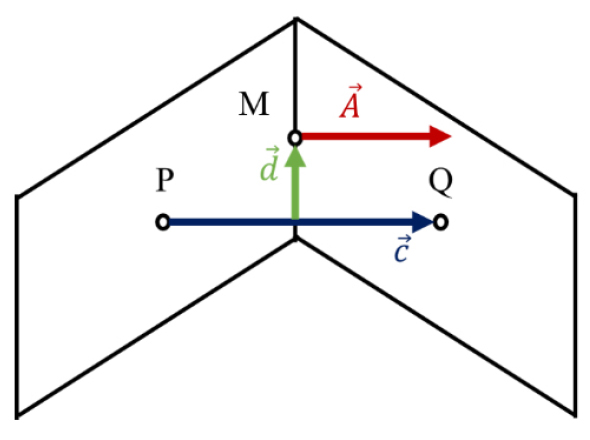
대상 공간을 유한개의 격자로 분할하여 수치 해석을 하는 CFD에서 격자는 중요한 설계 요소 중 하나이다. 설계된 격자의 적정성은 격자 품질 지표로 확인한다. 보편적으로 CFD 연구에서는 skewness와 non-orthogonality가 품질 지표로 사용된다(Fabritius and Tabor, 2016). Skewness는 유한체적 이산화 과정에서 발생하는 수치 확산 오류를 평가하는 지표이다. Skewness는 Figure 1과 같이 산정하며 계산식은 식 (1)과 같이 인접한 두 셀의 각각 중심점(P, Q)을 연결한 벡터()와 두 셀이 교차하는 지점의 중심점(M)에서 벡터와의 거리인 의 크기의 비율로 산정한다.
여기서, 는 skewness이다.
Non-orthogonality는 Figure 1와 같이 두 셀의 중심점을 연결한 벡터()와 두 셀의 교차하는 지점의 중심점 M에서의 법선 벡터() 사이의 각도를 의미한다. 좋은 품질의 격자계에서는 이 두 벡터는 평행을 이루고 있어야 한다. 그러나 이상적인 정육면체 격자계를 구성하지 않는 이상, 두 벡터의 평행성을 충족하기 어렵다. 한편, CFD는 Navier-Stokes 방정식의 해석 과정에 있어서 법선 벡터를 이용하여 셀 간의 플럭스를 계산한다. 따라서 정확한 해석 결과를 위해서는 non-orthogonality를 최소화하는 것이 중요하다. Non-orthogonality는 식 (2)와 같이 계산된다.
여기서, 는 non-orthogonality이다.
Skewness의 경우 최대 값을 품질 기준으로 활용하고 있다. CFD 소프트웨어 마다 계산하는 방식이 상이하여 기준이 조금씩 차이가 있으며 개방형 CFD 분석 도구인 OpenFOAM에서는 4를 초과하지 않아야 한다. Non-orthogonality 또한 최대 값을 품질 기준으로 적용하고 있으며, CFD 해석의 수렴성을 위해 70을 초과하지 않아야 한다.
격자 품질 예측 모델 개발 방법
격자 품질 예측을 위한 형상 특성 지표 선정
특정 대상의 기하학적 특성을 수치로 나타낸 형상 특성 지표는 다양한 학문 분야에서 활용되고 있다. 격자의 품질에 주요한 영향을 주는 형상의 특성 지표를 선정하고자 하였다. 분석 대상의 형상이 복잡할수록 격자의 생성 난이도가 증가하고 전반적인 품질 지표의 하락이 발생한다. 따라서 본 연구에서는 형상의 복잡도와 관련이 있는 inverse topology count, surface area to volume ratio, shape complexity의 총 3가지의 형상 특성 지표를 격자 품질 지표 예측에 활용하였다.
Inverse topology count (ITC)는 White et al. (2005)가 격자 생성 복잡도를 계산하기 위해 제시한 형상 특성 지표로 형상이 가진 면과 선의 수를 이용하여 산정한다. ITC는 항상 1보다 작거나 같으며, 식 (3)과 같이 계산된다.
여기서, F는 형상을 구성하는 총 면의 수, E는 형상을 구성하는 총 선의 수이다.
형상 모델을 구성하는 점, 선, 면 등의 위상정보가 많을수록 형상이 복잡해지고 이에 따라 격자 생성의 난이도가 상승한다. 격자 생성의 난이도가 높아질수록 육면체 격자계가 형성되기 어려우며 이는 격자의 품질 또한 저하될 가능성이 높다. 이와 같이 ITC는 형상 복잡도에 따른 격자 난이도를 설명하는 지표이며 격자 품질에 밀접한 연관이 있으므로 예측을 위한 지표로 활용하였다.
두 번째로 격자 품질 예측에 활용한 형상 특성 지표는 surface area to volume ratio (SAV)이다. 대상 형상을 구성하는 표면적을 부피로 나눈 값으로 식 (4)와 같이 계산된다.
여기서, A는 대상 형상의 표면적(m2), V는 대상 형상의 부피(m3)이다.
SAV는 화학 분야에서 고체 물질의 화학 반응성 산정이나 생물학 분야에서 단위 유기체의 형상적 특성을 표현하기 위해 자주 사용되는 지표이다. 또한 유체역학 분야에서는 SAV의 역수 형태를 특성길이로 정의하고 흐름 특성과 밀접한 관련이 있는 레이놀즈 수 계산에 활용하고 있다. 따라서 형상의 기하학적 특성을 판단할 수 있고, 유체의 흐름 특성을 나타내는 레이놀즈 수 계산에도 사용 가능하므로 격자 품질 예측 지표로 선정하였다.
이와 함께 Valentan et al. (2008)에서 제시한 shape complexity (SC)를 품질 예측에 활용하였다. SC는 부피를 총 면의 개수로 나누어 산정하며 식 (5)와 같이 계산된다.
같은 부피를 가진 형상이라도 구성하는 면의 수가 더 많은 모델이 위상 정보 또한 많이 가지고 있다. 이는 더 복잡한 형상 정보를 가진 것을 의미하며 나아가 격자 생성의 난이도 또한 높아짐을 의미한다. 따라서 SC도 격자 생성 난이도와 격자 품질에 영향을 주는 요인이므로 예측 인자로 활용하였다.
데이터셋 구축을 위한 CFD 모델 설계 방법
격자 생성 및 격자 품질 추출을 위하여 개방형 CFD 분석 도구인 OpenFOAM을 이용하여 CFD 모델을 설계하였다. 격자의 품질은 격자 크기, 격자의 형상, 분석 대상의 형상 등 다양한 요인에 의해 영향을 받게 된다. 본 연구에서는 분석 대상의 형상에서 추출할 수 있는 특성으로 격자 품질을 예측하고자 하였으며, 격자 조건의 경우 Lee et al. (2020)에서 제안한 특성길이별 적정 해상도를 적용하였다. 이를 통해 최적 격자 조건으로 분석 대상의 형상으로 격자 모델을 설계할 때 해당 격자 품질을 예측할 수 있다. 또한, 품질 예측 결과가 좋지 않을 경우 분석 대상 형상의 최적화가 필요함을 의미하므로 형상 최적화 진행 여부를 판단할 수 있다. 따라서 격자 품질 예측을 통해 형상 최적화 과정의 필요 여부를 판단하여 형상 최적화 과정에 소요되는 작업량과 시간을 절감 가능하다. 또한, 특성길이별 적정 해상도 조건에 대한 품질 예측을 통해 해당 해상도의 적합성을 판단하기 때문에 격자 독립성 검정으로 인해 발생하는 반복 작업을 최소화할 수 있다.
격자의 형상은 고품질의 격자를 구성할 수 있는 육면체 격자를 사용하였다. 격자의 크기는 Table 1과 같이 Lee et al. (2020)에서 도출한 대상의 특성길이별 최적 격자 해상도를 사용하였다. 여기서 특성길이는 대상의 체적을 표면적으로 나눈 값으로 SAV의 역수이다. 육면체 격자 구성 방법과 특성길이별 최적 격자 해상도를 적용하여 분석 대상별 최적 격자 모델을 설계하였다. 이와 같이 설계된 각 대상별 격자의 품질을 추출하여 다중선형회귀 분석을 위한 데이터를 구축하였다.
Table 1.
Optimal grid resolution by characteristic length
| Characteristic length (CL) | Optimal grid resolution |
| CL ≤ 0.3 | 8 |
| 0.3 ≤ CL ≤ 0.5 | 16 |
| 0.7 ≤ CL | 24 |
다중선형회귀분석을 통한 격자 품질 예측 모델 구축 방법
건물의 형상 특성 지표를 이용하여 격자의 품질을 예측할 수 있는 모델 개발을 위하여 다중선형회귀분석을 시행하였다. 케이스 스터디를 통해 구축한 총 37개의 격자 품질 결과를 기반으로 회귀분석을 하였다. 종속변수는 최대 non-orthogonality, 최대 skewness의 2가지로 설정하였다. 독립변수는 ITC, SAV, SC의 형상 특성 지표 3가지로 설정하였다.
단일 형상 특성 지표가 격자 품질에 미치는 영향 또한 함께 분석을 수행하였다. 각 개별 특성 지표들이 개별 격자 품질 지표에 미치는 영향을 분석한 후, 다중선형회귀분석을 실시하였다. 다중선형회귀분석은 각 종속변수별로 수행하여 2개의 품질 지표 예측식을 도출하였다. 이를 통해 별도의 CFD 모델링 과정 없이 형상의 단순화 과정 적용 유무를 판단할 수 있는 격자 품질 예측 모델을 개발하였다.
격자 품질 예측 모델 도출 결과
대상 시설 및 형상 특성 지표 산정
다중선형회귀분석을 위한 데이터셋을 구축하기 위해 대상 시설 선정 및 형상 특성 지표 계산을 수행하였다. 다양한 건축물에서 형상 특성에 따른 격자 품질 도출 결과를 구축하기 위하여 본 연구는 Park et al. (2020)에서 사용한 BIM 라이브러리를 활용하여 37개의 건물 모델을 대상 시설로 선정하였다. 대상 시설의 특성길이 범위가 최소 0.3부터 최대 1.1까지로 다양한 형상 특성을 반영하였다. 각 대상 시설별 기하학적 특징은 Table 2와 같다.
Table 2.
Geographical information of the geometry dataset
| Volume (m3) | Surface area (m2) | Characteristic length (m) | |
| Average | 170.7 | 214.0 | 0.7 |
| Minimum | 10.5 | 34.3 | 0.3 |
| Maximum | 1052.4 | 985.8 | 1.1 |
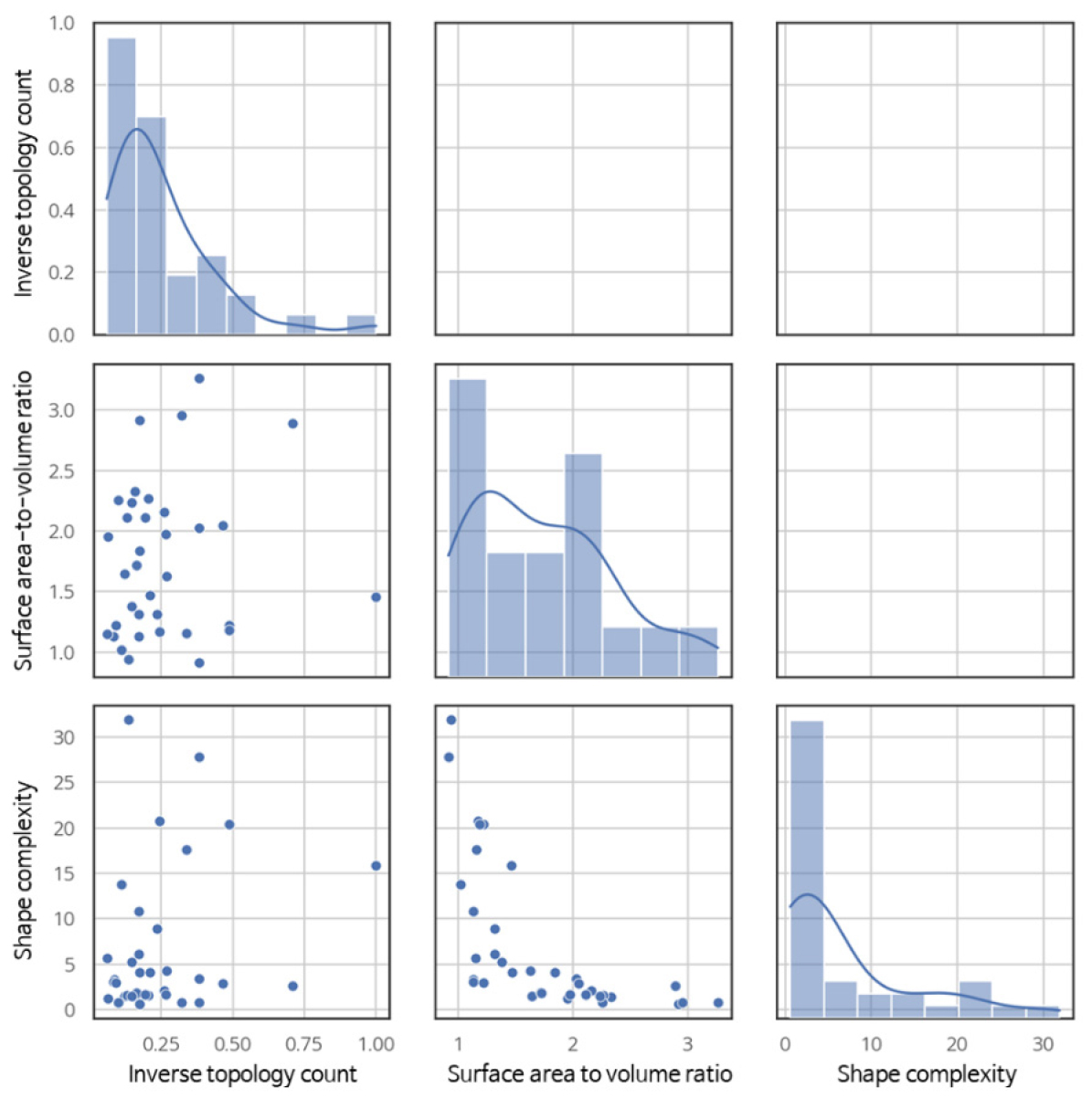
선정된 37개의 대상 시설별로 형상 특성 지표를 산정하였으며, 지표별 분포 결과는 Figure 2와 같다. ITC의 경우 대부분 0.25 이하에 분포하는 것으로 나타났다. ITC는 1에 가까울수록 정육면체와 비슷한 단순한 모형임을 의미하는데 건축물 형상의 경우 돌출부, 기둥, 창, 문, 곡면부 등 형상의 복잡도를 높이는 요소들이 다양하게 존재하기 때문에 대부분 낮은 값으로 분포하였다. 또한 ITC는 SAV나 SC와 연관성은 없는 것으로 나타났다.
SAV는 대상 시설의 부피가 커질수록 작은 값을 도출하게 된다. 본 연구에서 다양한 부피를 가진 건축물 형상을 대상으로 하여 SAV 역시 1~3 사이로 분포하는 것으로 나타났다. 한편, SAV와 SC는 대상 시설의 부피를 계산 인자로 사용하기 때문에 연관성이 ITC 보다는 다소 높게 도출되었다.
마지막으로 SC는 동일 부피 대비 면의 개수가 적을수록 값이 높게 도출되는데 이는 단순한 형상일수록 SC 값이 높게 나타남을 의미한다. 그러나 건축물 형상의 경우 ITC에서 언급한 바와 같이 다양한 요소들이 존재하기 때문에 형상의 복잡성이 큰 특성이 있다. 이러한 이유로 본 연구의 SC 분포 역시 대부분 5이하로 낮은 값으로 형성됨을 알 수 있다. 또한 SC가 10 이상으로 도출되는 비교적 단순한 형태로 함께 존재하고 있어 다양한 건축물 형상 특성을 고려한 분석 및 예측 모델 도출이 가능한 것으로 판단되었다.
대상 시설별 격자 설계 및 품질 결과
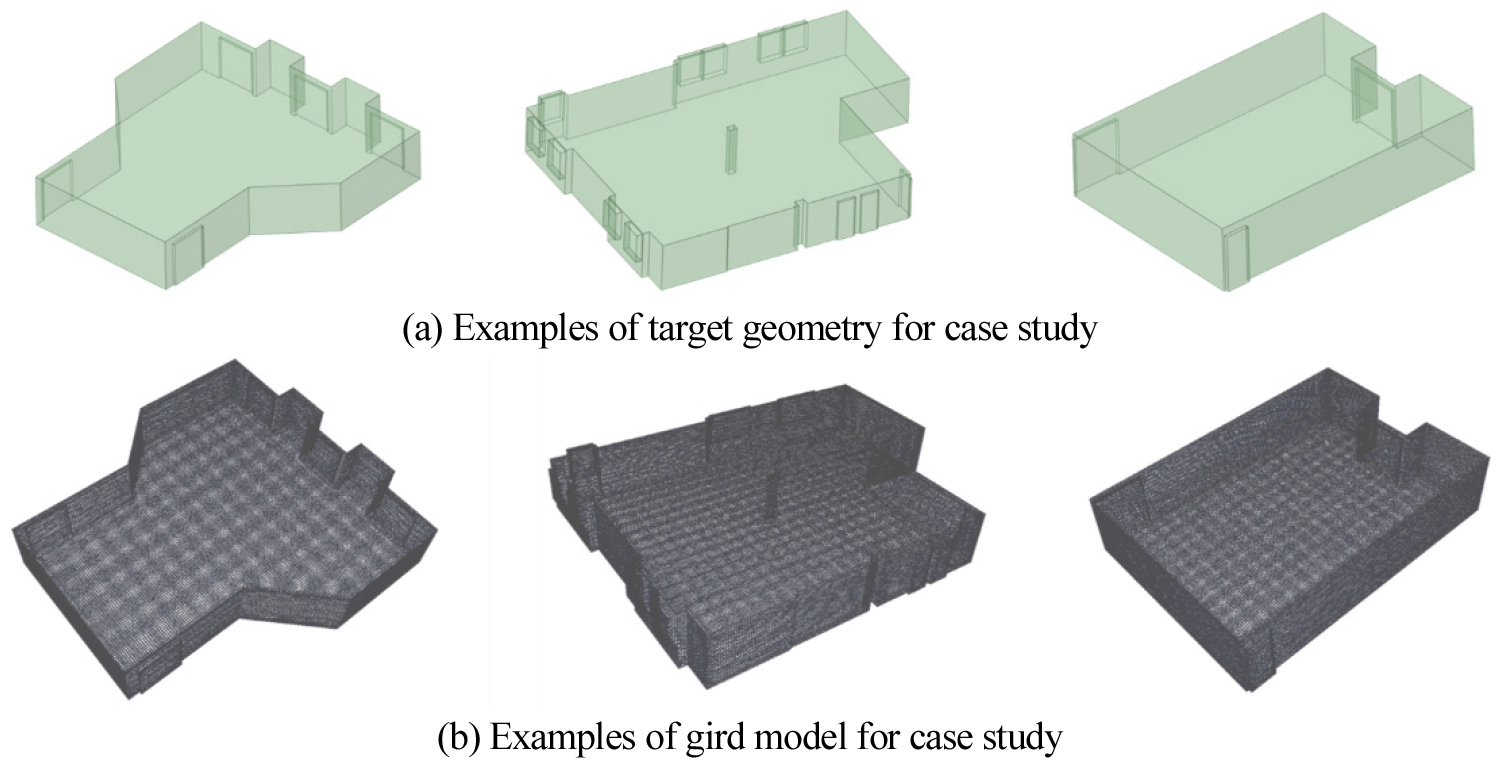
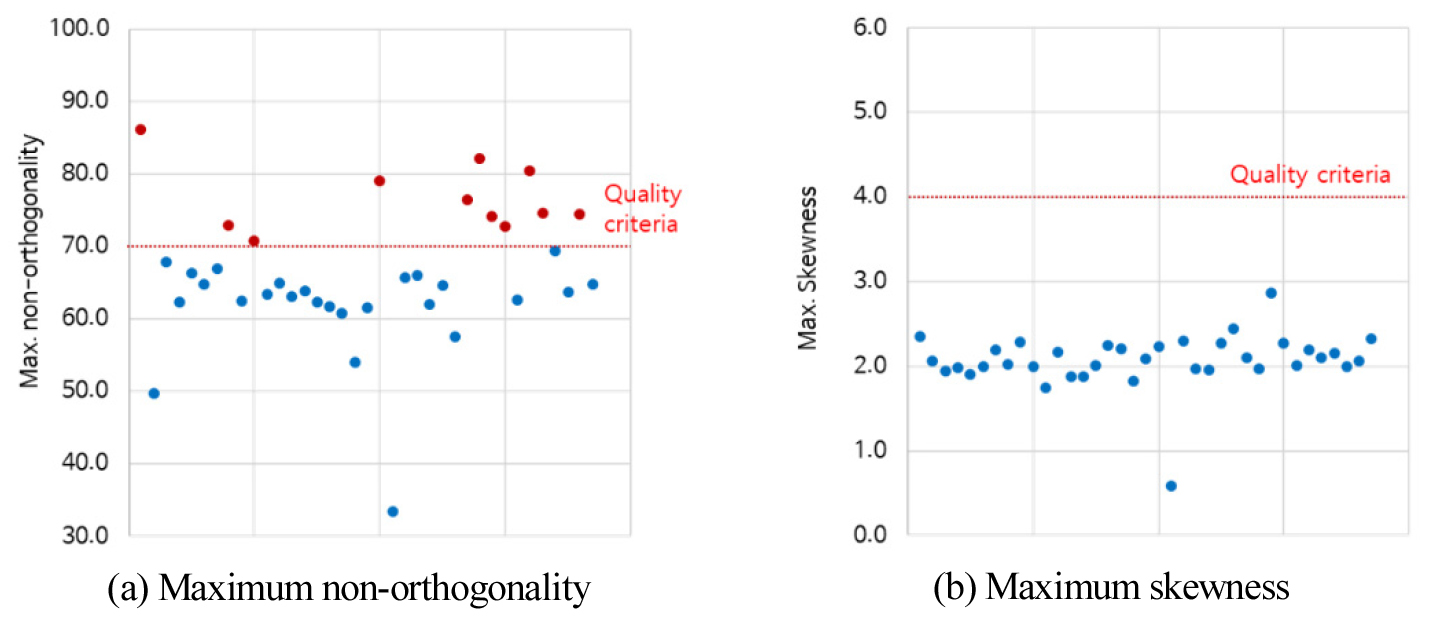
대상 분석 시설에 대하여 최적 격자 조건을 적용하여 격자를 생성하였으며, 이에 대한 격자 생성 결과는 Figure 3과 같으며 품질 지표 결과는 Figure 4와 같다. 최적 격자 해상도 조건을 적용하였음에도 최대 non-orthogonality는 기준치를 초과하는 케이스가 전체 중 약 30%로 나타났다. 해당 케이스들은 형상 자체가 매우 복잡하여 최적 격자 생성 조건을 적용하였음에도 품질이 저하되었다. 따라서 이러한 케이스들은 형상 단순화 과정을 반드시 적용해야 한다.
최대 skewness에 대한 결과는 Figure 3의 (b)와 같다. 최대 skewness의 경우 대부분 케이스에서 약 2.1에 근사한 값을 도출하고 있으며, 품질 기준(4 이하)은 모든 케이스에서 충족하고 있다. 형상의 특성은 다르지만 모든 케이스에서 육면체 격자 형상과 최적 격자 크기를 적용하여 skewness 지표가 낮게 형성된 것으로 판단된다. 즉, skewness 지표는 대상의 형상보다 격자의 형상과 크기에 더 영향을 받는 것으로 도출되었다.
형상 특성 지표별 격자 품질 영향 분석
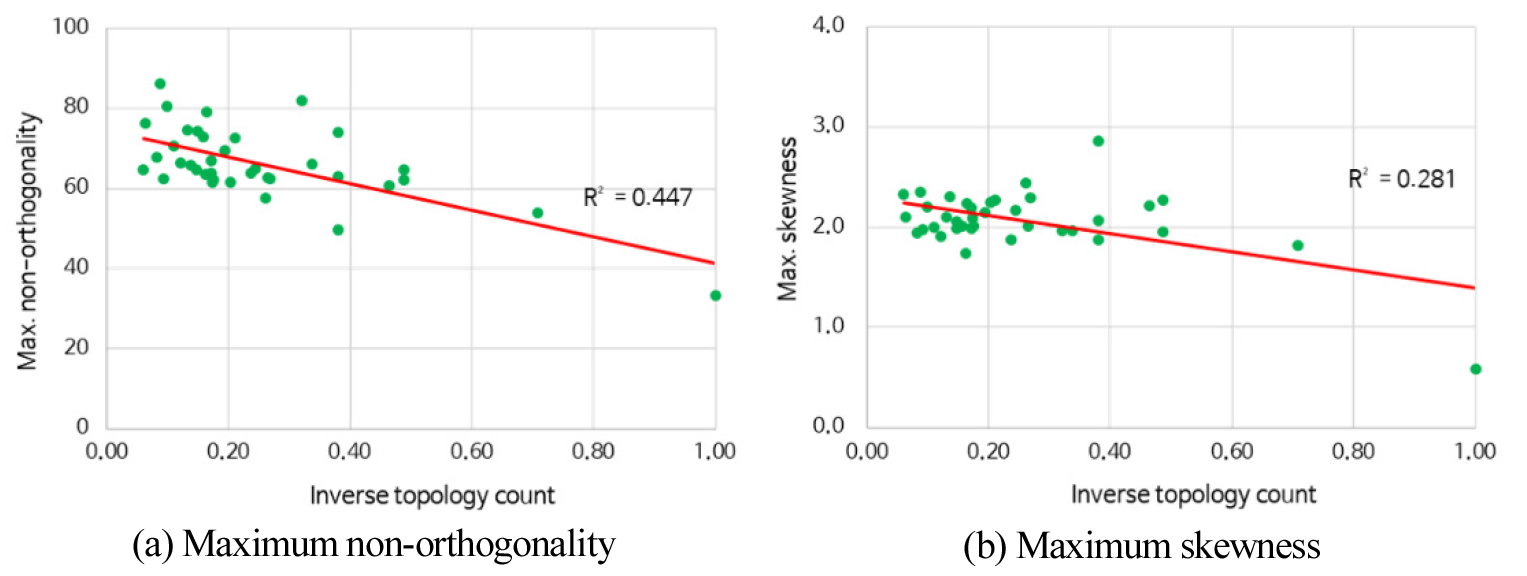
케이스 스터디를 통해 도출한 각 형상 특성 지표와 이에 따른 격자 품질의 분포를 분석한 결과로 Figure 5, 6, 7과 같다. Figure 5는 ITC와 최대 non-orthogonality와 최대 skewness 격자 품질 지표에 미치는 영향을 나타낸 그림이다. Figure 5의 (a)에서 볼 수 있듯이, ITC는 최대 non-orthogonality와 음의 상관관계를 가지고 있는 것으로 도출되었다. 해당 분포에 대한 선형 추세선의 경우 약 45%의 설명력을 가지는 것으로 도출되었다. ITC 값이 증가할수록 단순한 형상이며 이로 인하여 격자의 품질이 개선되어 나타난 결과로 사료된다. 최대 skewness는 Figure 5의 (b)와 같이 ITC에 대한 설명력이 약 28%로 최대 non-orthogonality에 비해 상관 관계가 약한 것으로 도출되었다.
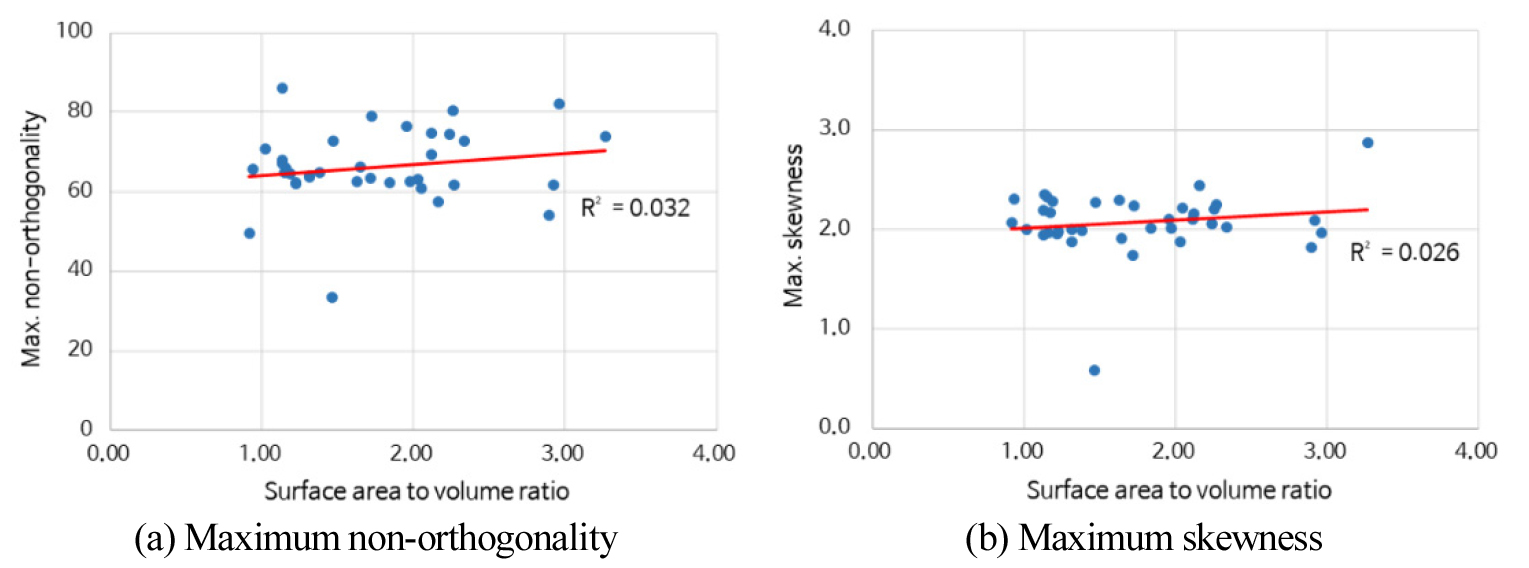
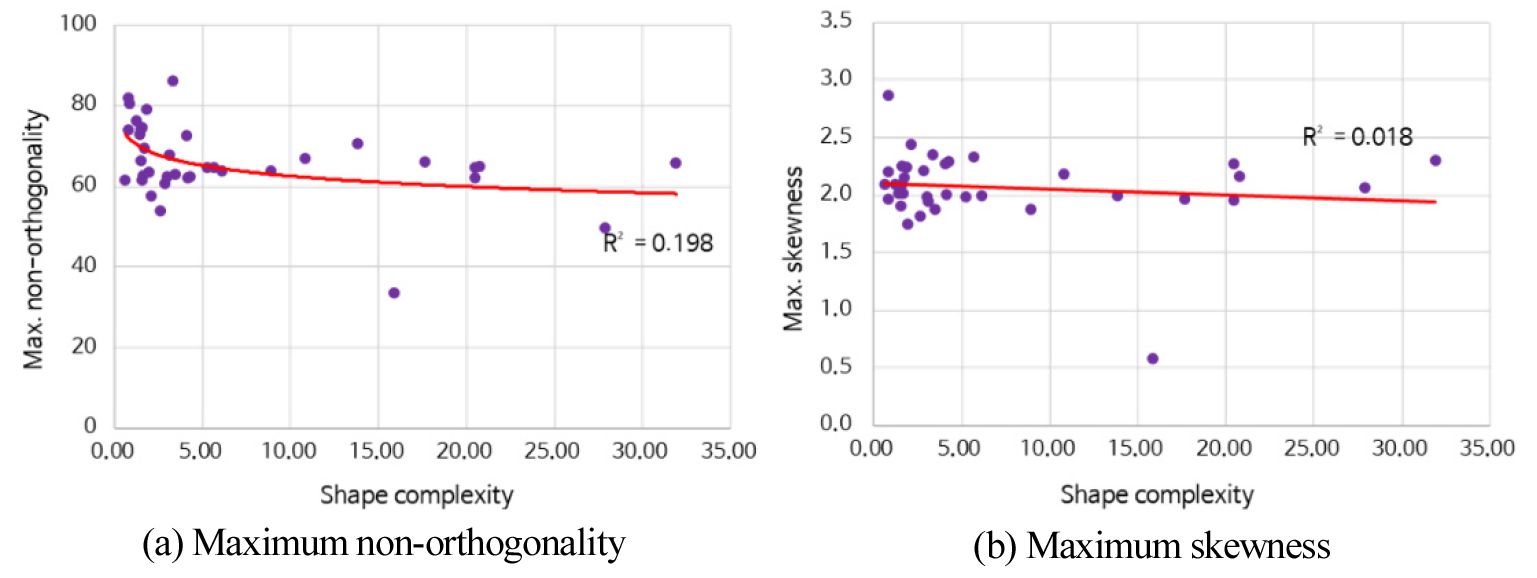
Figure 6은 SAV에 따른 품질 지표 분포 결과이다. ITC와 달리 최대 non-orthogonality에 대하여 상관성이 약한 것으로 도출되었다. Figure 6의 (a)와 같이 SAV와 상관없이 최대 non-orthogonality가 분포하고 있다. 최대 skewness 또한 Figure 5의 (b)와 같이 유사한 경향으로 나타났다. Figure 7은 SC에 대한 결과이다. SAV와 유사하게 최대 non-orthogonality와 최대 skewness 지표에 대해 높은 영향력이 나타나지 않았다. 단일 형상 지표의 격자 품질 예측에 대한 결과를 정리하면 Table 3과 같다. ITC를 이용하는 경우 R2가 품질 지표별로 각각 0.447, 0.281로 다른 두 지표에 비해 높게 도출되었으나 예측 모델로는 설명력이 다소 부족하다. 나머지 두 형상 지표의 경우 R2가 0.2 이하로 매우 낮게 도출되었다. 따라서, 3개 형상 특성 지표 모두 단일로 사용하여 격자 품질을 예측하기에는 설명력이 부족하며 다중선형회귀분석을 통한 예측 식 도출이 필요한 것으로 나타났다.
Table 3.
R2 of grid quality prediction using single geometry characteristic index
| ITC | SAV | SC | |
| Maximum non-orthogonality | 0.447 | 0.032 | 0.198 |
| Maximum Skewness | 0.281 | 0.026 | 0.018 |
다중회귀분석을 통한 격자 품질 예측 모델 도출
예측 모델의 결정력을 높이기 위해 최대 non-orthogonality은 역수 변환을 적용하였으며, 위해 최대 skewness의 경우 로그 변환을 적용하였다. 이와 함께 독립변수에 각 형상 특성 지표의 제곱항을 추가하여 2차 다항식 회귀모델에 대한 분석을 수행하였다. 각 품질 지표에 대한 결과는 Table 4, 5와 같다.
Table 4.
Regression analysis of reciprocal-transformed maximum non-orthogonality
| Multiple R2 | Adjusted R2 | F-statistic | p-value |
| 0.752 | 0.738 | 51.58 | < 5.03e-11 |
| Coefficient | Standard error | p-value | |
| (Intercept) | 0.0150 | 0.000 | < 0.001 |
| ITC2 | 0.0141 | 0.001 | < 0.001 |
| SAV2 | -0.0003 | 0.000 | < 0.014 |
Table 5.
Regression analysis of log-transformed maximum skewness
최대 non-orthogonality에 대한 분석 결과, SC에 대한 영향이 통계적으로 유의하지 않아 제외하였으며, 최종적으로 ITC의 제곱항과 SAV의 제곱항이 유의한 인자로 도출되었다. 예측식은 식 (6)과 같다. 최대 non-orthogonality의 경우 Figure 4와 같이 ITC와 강한 음의 상관관계가 있어 예측 식에도 이와 같은 경향이 나타났다. 최대 non-orthogonality에 대한 예측 식의 adjusted R2이 0.738로 양호한 결정력을 갖고 있으며 예측 모델에 대한 p-value도 통계적으로 유의한 수치로 나타났다.
여기서, 는 최대 non-orthogonality이다.
최대 skewness에 대한 회귀 분석 결과는 Table 5와 같다. 최대 non-orthogonality와 동일하게, SC는 통계적으로 유의하지 않아 예측 모델에서 제외하였다. SC의 경우 품질 지표 모두 유의한 인자로 도출되지 않았다. 이는 Figure 2와 같이 SAV와 높은 연관성으로 인해 유의한 인자에 제외되는 것으로 사료된다. 예측식은 식 (7)과 같다. 이와 함께 최대 skewness의 경우 adjusted R2이 0.806이며, 예측 모델에 대한 p-value 역시 통계적으로 유의한 수치로 나타났다.
여기서, 는 최대 skewness이다.
결 론
고품질의 격자 모델을 설계하기 위한 복잡한 과정과 시행착오를 줄이기 위해 본 연구에서는 형상 특성 지표를 활용하여 건물 CFD 모델의 격자 품질 예측 모델을 개발하였다. 격자 품질에 영향을 주는 예측 인자를 선정하고자 하였으며, ITC, SAV, SC의 3가지 형상 특성 지표를 선정하였다. 케이스 스터디를 통해 특성 지표가 격자 품질에 미치는 영향을 파악하고 다중선형회귀분석을 통해 예측 모델을 개발하였다.
예측 모델 개발을 위하여 37개의 대상 시설에 대하여 케이스 스터디를 수행하였다. 이와 함께 형상 특성 지표별로 격자 품질에 미치는 영향을 분석하였으며, ITC의 경우 최대 non-orthogonality와 높은 상관성이 확인되었다. 케이스 스터디 결과를 활용하여 다중선형회귀분석을 실시하였고 이를 통해 격자 품질 예측 모델을 개발하였다. 격자 품질별로 예측 모델을 도출하였으며 모두 통계적으로 유의한 것으로 평가되었다. 최대 non-orthogonality에 대한 예측 모델의 adjusted R2은 0.738, 최대 skewness에 대한 예측 모델의 adjusted R2은 0.806으로 도출되었다. ITC와 SAV는 품질 지표 예측식에 모두 유의한 인자로 도출되었으나, SC의 경우 품질 예측에 유의한 인자로 도출되지 않았다.
본 연구에서는 기존 사례가 없는 격자 품질 예측 모델 개발하였으며, 연구 결과 형상 특성 지표를 이용한 예측 결정력이 품질 지표별로 각각 73.8%, 80.6%로 도출되었다. 이를 통해 특성 지표를 통한 격자 품질 지표 예측 가능성을 확인할 수 있었다. 또한, SC를 제외한 두 지표는 예측 모델에 모두 유의한 인자로 도출되어 품질 예측에 적합하다는 것을 확인하였다. 한편 본 연구에서는 개방형 CFD 분석 도구인 OpenFOAM을 통해 육면체 격자계에 대한 품질 예측을 수행하였다. 그러나 복잡도가 높은 건축물 형상에 대해서는 육면체 격자 설계가 불가능하여 사면체, 프리즘 격자 등이 적용되어야 할 수 있다. 따라서 향후 연구에서는 위와 같은 다양한 격자 형상에 대한 품질 예측도 수행할 예정이다. 이와 함께 향후 연구에서는 케이스 및 인자 추가, 기계 학습 등을 이용하여 예측 모델의 결정력을 향상시키고 검증을 진행하여 예측 모델을 신뢰성을 확보할 예정이다.