Analysis of the Impact of Extended Data Point Measurement Time on Uncertainty in the Blower Door Test

Ji-Hoon Choi; Ji-Hye Kim

doi:10.22696/jkiaebs.20240035

Preview

Research Article

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems. 30 October 2024. 412-427
https://doi.org/10.22696/jkiaebs.20240035

Analysis of the Impact of Extended Data Point Measurement Time on Uncertainty in the Blower Door Test

블로어도어 실험의 데이터 포인트 측정시간 연장에 따른 불확도 영향 분석

Ji-Hoon Choi¹

Ji-Hye Kim²^*

최 지훈¹

김 지혜²^*

¹Master Course Student, Department of Architectural Engineering, Graduate School, Kwangwoon University, Seoul, Korea

²Assistant Professor, Department of Architectural Engineering, Kwangwoon University, Seoul, Korea

¹광운대학교 일반대학원 건축공학과 석사과정

²광운대학교 공과대학 건축공학과 조교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Uncontrolled air leakage through windows and cracks in buildings is referred to as infiltration, which leads to increased heating and cooling energy consumption and deteriorates indoor air quality. The airtightness performance of a building is primarily evaluated using the pressurization method with a blower door, and the reliability of this evaluation is determined by the flow exponent(n) and the coefficient of air leakage (C_L) derived from the test. However, blower door tests are subject to variability in measurements due to factors such as external wind speed and indoor-outdoor temperature differences. So, previous researchers have extended the measurement time of Zero-flow pressure difference or proposed new regression methods such as Weighted Line of Organic Correlation (WLOC) and Iterative Weighted Least Squares (IWLS) to reduce measurement uncertainty. This study analyzed how extending the measurement time of data points and applying WLOC improves the reliability of airtightness measurements.

Keywords

Blower door test

Airtightness

Uncertainty

Regression method

OLS

WLOC

키워드

블로어도어 실험

기밀성능

불확도

회귀방법

OLS

WLOC

MAIN

서 론
회귀 분석방법
Ordinary least squares method (OLS)
Weighted line of organic correlation method (WLOC)
측정개요
측정 장소 개요
측정절차 및 조건
측정결과
측정 데이터
기밀성능 매개변수 분석결과
기밀성능 매개변수의 관측 확장불확도와 계산 확장불확도 비교
결 론

서 론

건물의 창호나 구조체 틈새를 통한 제어되지 않은 공기의 유입과 출입을 각 침기와 누기라고 한다. 침기와 누기의 양이 많을수록 냉·난방에너지 사용량이 증가하고, 외부 오염물질의 실내 유입으로 실내 공기질이 저하되는 등 건물에 다양한 문제를 일으킬 수 있다. 이는 실내·외 온도차와 바람의 영향 등 환경조건에 의해서 영향을 받으나 건물의 기밀성능에 따라 동일한 환경조건이더라도 양이 달라지므로 건물 에너지와 환경성능을 제대로 파악하기 위해서는 건물의 기밀성능 평가가 선행되어야 한다.

건물 기밀성능의 평가는 블로어도어를 활용한 가·감압법(Pressurization and Depressurization Method)이 주로 적용되고 있다. 이 방법은 블로어도어를 사용하여 측정대상 공간을 가압 또는 감압하여 다양한 실내외 압력차에 대한 유량을 측정한다. 이후 복수 개의 데이터 포인트에서 측정된 압력차와 유량 데이터를 선형 회귀 분석하여 대상 공간의 기밀성능 매개변수 n (flow exponent)과 C_L (Coefficient of air leakage)를 도출한다. 기밀성능은 도출된 매개변수를 바탕으로 압력차와 유량의 관계를 나타내는 멱승법칙(Power-law equation)을 통해 계산되기 때문에 n과 C_L값을 정확하게 추정하는 것이 건물 기밀도 평가의 신뢰도를 확보하는 데 중요한 역할을 한다.

그러나, n과 C_L값을 추정하기 위한 블로어도어 실험은 외부풍속, 실내·외 온도 차, 측정 장비, 측정자, 회귀방법 등 다양한 요인으로 인해 오차가 발생한다(Choi et al., 2014; Hurel and Leprince, 2021; Kim et al., 2022; Mélois et al., 2022). 오차는 측정 장비, 측정자 등과 같이 원인을 알 수 있고 일련의 관측값에 항상 같은 방향과 같은 크기로 발생하는 계통 오차(systemic error)와 크기, 방향이 불규칙한 우연 오차(random error)로 구분할 수 있다. 계통 오차는 보정치를 통해 보완할 수 있으나, 우연 오차는 측정 과정에서 예측할 수 없는 요인으로 인해 오차가 발생하므로 반복 측정한 결과를 통계적으로 처리한다. 측정결과의 신뢰도를 높이기 위해서는 오차 요인을 최대한 통제하고 반복 측정함으로써 오차를 줄이는 것이 가장 바람직하나 우연 오차와 같이 제어가 불가능한 오차 요인이 존재하고 상황에 따라 반복 측정이 어려운 경우도 빈번하다. 따라서 다양한 오차 요인을 체계적으로 고려하고 측정결과의 신뢰성을 정량적으로 표현하는 불확도 평가는 매우 중요하다. 이를 통해 측정결과가 실제 상황에서 얼마나 정확하게 적용될 수 있는지를 판단하고, 연구결과의 재현성을 높이는 데도 기여할 수 있다.

Prignon et al. (2019)은 기밀도 측정 시 차압 보정에 사용되는 영(0) 기류 압력차(팬을 정지한 상태에서 측정한 차압) 측정시간 연장에 따른 불확도를 평가하였다. Prignon은 영(0) 기류 압력차 측정시간 증가에 따라 불확도가 감소하는 것을 확인하고, 측정 신뢰도를 높이기 위해 영(0) 기류 압력차 측정시간을 30초 연장하는 방안을 제안하였다. Delmotte (2017)와 Okuyama and Onishi (2012)는 기밀도 측정값의 불확도를 반영하여 데이터를 피팅하는 새로운 회귀방법을 제안하였다. 기존의 Ordinary Least Squares (OLS)는 x축 데이터(압력차)의 불확도를 무시하고, y축 데이터(유량)는 불확도가 동일하다는 가정으로 데이터를 피팅하는 회귀방법인 반면에 Delmotte (2017)가 제안한 Weighted Line of Organic Correlation (WLOC)와 Okuyama and Onishi (2012)가 제안한 Iterative Weighted Least Squares (IWLS)는 압력차와 유량 데이터의 불확도를 반영해 데이터를 피팅하기 때문에 특정 환경조건에서 OLS 방법보다 모수를 더 잘 추정하는 것을 확인하였다. Prignon et al. (2020)은 동일한 조건에서 반복 측정한 데이터를 OLS, WLOC, IWLS 방법으로 피팅하여 구한 관측 확장불확도(반복 측정값으로 추정한 모평균 신뢰구간, A형 불확도 평가)와 계산 확장불확도(개별 측정값으로 추정한 모수 추정 신뢰구간, B형 불확도 평가)를 서로 비교하였다. 비교 결과, WLOC와 IWLS로 구한 계산 확장불확도는 관측 확장불확도의 신뢰구간 범위 내에 있었으나 OLS로 구한 계산 확장불확도는 관측 확장불확도의 신뢰구간을 일부 벗어나는 것으로 확인되었다. 그리고 IWLS와 WLOC 방법은 불확도 계산 결과가 유사한 수준이지만 IWLS 방법은 반복적인 가중치 갱신과 매개변수 재추정 과정으로 인해 WLOC보다 수식이 길고 복잡하여 WLOC 방법이 더 효율적임을 확인할 수 있었다.

선행연구에서 영(0) 기류 압력차 측정시간을 연장하여 정확도를 향상한 것처럼, 블로어도어 실험에서 데이터 포인트(x-value는 각 압력차 y-value는 해당 압력차에 대응되는 유량 데이터를 나타내는 점) 측정시간을 연장하면 해당 포인트에서 측정되는 대표값의 불확도를 낮추는 데 영향을 줄 것으로 기대된다. 그리고, 각 데이터 포인트의 불확도를 이용해서 회귀선을 찾는 WLOC를 적용하면 기밀도 측정값의 신뢰도를 향상할 수 있을 것으로 판단되며, 이는 반복 측정이 어려운 상황에서 개별 측정값으로 추정한 모수 추정 신뢰구간이 모평균 신뢰구간을 벗어나지 않도록 기여할 것으로 예상한다. 본 연구에서는 OLS와 WLOC 방법으로 추정한 매개변수가 데이터 포인트 측정시간 연장에 따라 어떻게 변화하는지 살펴봄으로써 데이터 포인트 측정시간 연장이 매개변수 추정에 미치는 영향을 살펴보았다. 그리고 같은 공간에서 블로어도어 실험을 31회 반복수행한 후, 반복 측정값으로 구한 매개변수의 관측 확장불확도와 31개의 개별 측정으로 계산한 계산 확장불확도를 각각 OLS와 WLOC 방법으로 구한 결과를 비교함으로써 관측 확장불확도를 더 잘 추정하는 회귀방법에 대해 알아보았다. 본 연구의 목적은 블로어도어 실험에서 데이터 포인트 측정시간의 연장이 불확도에 미치는 영향을 회귀방법에 따라 분석하는 것이다.

회귀 분석방법

차압에 따른 누기량은 식 (1)과 같은 멱승법칙으로 나타낼 수 있다. 여기서 Q_env,i는 외피를 통하는 유량을, △p_i는 실내·외 압력차를 의미하며, i는 N개의 데이터 포인트 중 i번째 데이터 포인트를 나타낸다. 식 (1)의 양변을 로그 변환하면(식 (2)), 1차 함수 형태로 변환되어 식 (3)과 같이 선형화할 수 있다. 이후, N개의 데이터 포인트에 대해 회귀 분석을 수행하면 회귀선의 기울기 a와 절편 b를 추정할 수 있다. 기울기 a는 매개변수 중 하나인 n에 해당하고, 나머지 매개변수 C_L은 식 (4)과 같이 C_env값에 표준온도(T_o)와 실외온도(T_e)를 사용하여 온도에 따른 공기 밀도 변화를 보정하여 산출한다.

(1)

Q_{e n v, i} = C_{e n v} ∙ (∆ p_{i})^{n}

(2)

\ln (Q_{e n v, i}) = n ∙ l n (∆ p_{i}) + \ln (C_{e n v})

(3)

y_{i} = a ∙ x_{i} + b, a = n, b = \ln (C_{e n v})

(4)

C_{L} = C_{e n v} {(\frac{T_{0}}{T_{e}})}^{1 - a}

Ordinary least squares method (OLS)

OLS는 식 (5)과 같이 측정된 y_i값과 추정된 ŷ_i값 간 수직 거리의 제곱 합을 최소로 하는 회귀선을 추정한다. 이때, 기울기 a와 절편 b는 x_i와 y_i에 대해 편미분한 식을 연립하여 구한다(식 (6) 참조).

수식에서 $\sum x_{i}$ 은 $\sum_{i = 1}^{N} x_{i}$ 을 단순화하여 나타낸 것이다.

(5)

\sum (y_{i} - {\hat{y}}_{i})^{2} = \sum (y_{i} - a x_{i} - b)^{2}

(6)

a = \frac{N \sum x_{i} y_{i} - \sum x_{i} \sum y_{i}}{N \sum x_{i}^{2} - (\sum x_{i})^{2}}, b = \frac{N \sum x_{i}^{2} \sum y_{i} - \sum x_{i} \sum x_{i} y_{i}}{N \sum x_{i}^{2} - (\sum x_{i})^{2}}

Weighted line of organic correlation method (WLOC)

WLOC는 식 (7)과 같이 측정값과 추정치 간 수평·수직 차의 곱을 최소화하는 선형 방정식을 구하는 방법이다. WLOC는 OLS와 달리 복수의 데이터 포인트에서 불확도가 큰 데이터의 기여도를 낮추기 위해 식 (8)의 가중치를 도입하는데, 이 가중치는 각 데이터 포인트에서 측정된 ln (△p_i)와 ln (Q_env,i)의 표준편차의 역수를 사용한다. 따라서, 표준편차가 클수록 가중치가 줄어들어 표준편차가 큰 데이터 포인트의 회귀 식에 대한 영향력은 감소하고, 결과적으로 신뢰도가 높은 데이터 포인트들이 회귀선 도출에 더 큰 기여를 하게 된다. 이에 따른 WLOC에 의한 회귀선의 a와 b는 식 (9)과 같다.

(7)

\sum (v_{i} | x_{i} - {\hat{x}}_{i} | ∙ w_{i} | y_{i} - {\hat{y}}_{i} |) = \sum (v_{i} |x_{i} - \frac{y_{i} - b}{a}| ∙ w_{i} | y_{i} - a x_{i} - b |)

(8)

여기서, v_{i} = \frac{1}{s (x_{i})} = \frac{1}{u (x_{i})}, w_{i} = \frac{1}{s (y_{i})} = \frac{1}{u (y_{i})} s (x_{i}) 는 x_{i} 의 표 준 편 차

(9)

a = \frac{\sum v_{i} w_{i} y_{i} - b \sum v_{i} w_{i} x_{i}}{\sum v_{i} w_{i}}, b = \sqrt{\frac{\sum v_{i} w_{i} \sum v_{i} w_{i} y_{i}^{2} - (\sum v_{i} w_{i} y_{i})^{2}}{\sum v_{i} w_{i} \sum v_{i} w_{i} x_{i}^{2} - (\sum v_{i} w_{i} y_{i})^{2}}}

측정개요

측정 장소 개요

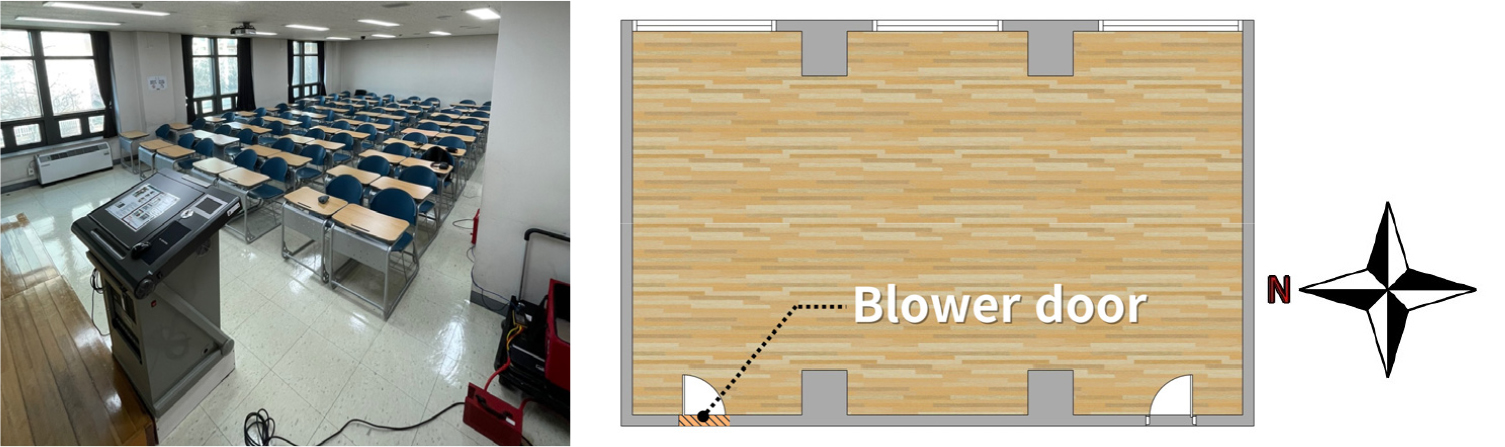
서울에 위치한 대학교의 한 강의실을 대상으로 블로어도어 실험을 수행하였다. 대상 건물은 철근 콘크리트 구조로, 2001년에 시공되었다. 건물 형태는 가운데 중정이 있는 ‘ㄷ’자 형태로 ‘ㄷ’자의 내측 면은 복도 ‘ㄷ’자 외측 면은 강의실 또는 연구실이 배치되어 있다. 건물은 총 10층의 규모이며, 측정은 해당 건물 2층에 위치한 강의실에서 진행하였다. 측정 장소의 사진과 평면도, 건물의 개요는 Figure 1, Table 1에 제시하였다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-05/N0280180502/images/Figure_KIAEBS_18_5_02_F1.jpg

Figure 1.

Photo and floor plan of test room

Table 1.

Summary of measurement site

Category	Description
Building use	Lecture Room
Year of completion	2001
Number of floors	2^{^nd} of 10 floors
Building structure	Reinforced concrete
Envelope	Punched window
Room area [m^²]	82.1
Room height [m]	2.5

측정절차 및 조건

본 연구의 측정절차는 ISO 9972 (2015)의 제시 조건에 따라 진행되었다. 측정 장비는 Retrotec 6000을 사용하였으며 팬 성능은 50 Pa에서 13,082 m³/h, 정확도는 ±5%이다. 온도 측정은 Lutron의 온·습도 측정 장비를 실내와 실외에 각 1개씩 설치하였으며, 장비의 정확도는 ±0.8℃이다. 외부풍속은 testo의 난류 측정 프로브를 사용하여 측정하였고, 해당 기기의 측정오차는 0.03 m/s, 분해능은 0.01 m/s이다. 반복 측정을 위해 측정마다 측정 장비의 설치 위치와 설정 조건을 같게 하고, 실내의 모든 창문은 닫고, 인접한 복도를 외부 기압과 동일하게 유지하기 위해 복도 창문을 모두 개방한 후 측정을 수행하였다(Figure 2 참조).

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-05/N0280180502/images/Figure_KIAEBS_18_5_02_F2.jpg

Figure 2.

Installation of measurement equipment and test environment

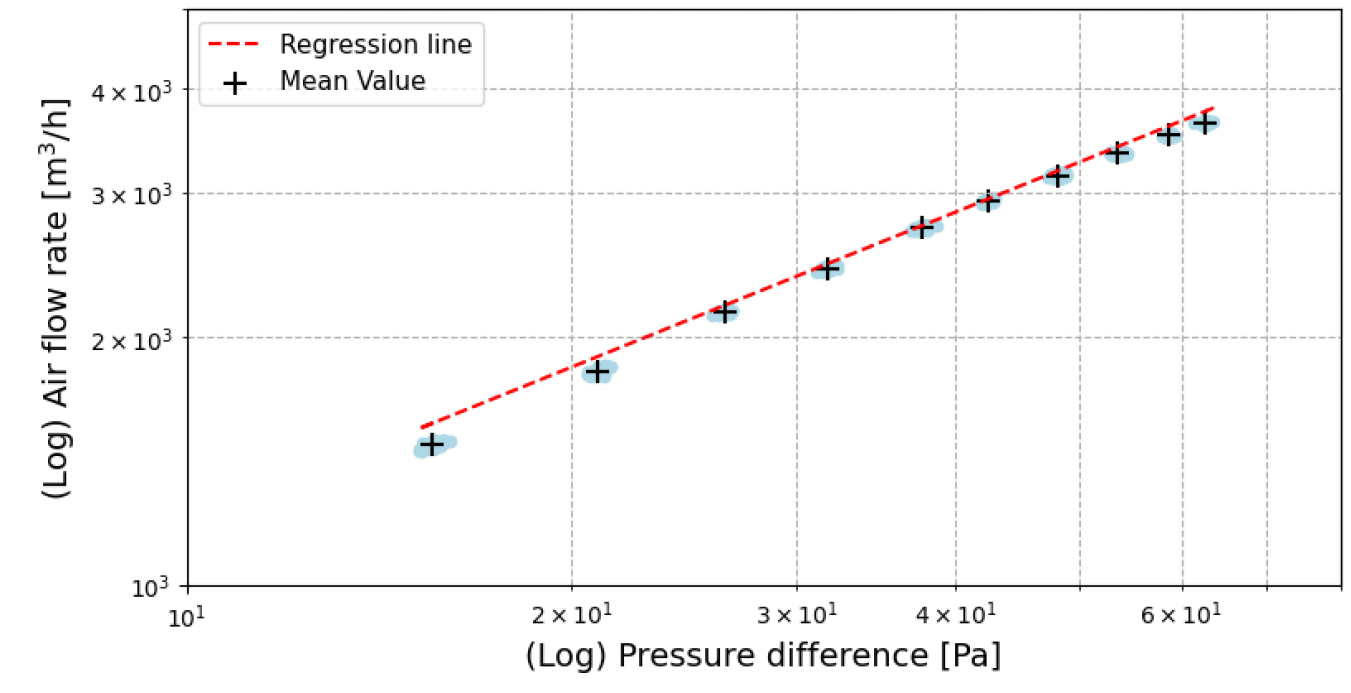
측정 기간은 2024년 1월부터 2월까지였으며, 측정 동안의 실내외 온도와 외부풍속 조건은 부록의 Table A1과 같다. 외부풍속은 2시간 동안 기록된 데이터를 평균화하였고, 온도는 측정 전·후 각각 20분 동안 측정된 값을 사용하였다. 영(0) 기류 압력차는 가·감압 전과 후에 기록하고 이후 압력차 보정에 적용하였다. 압력차에 따른 유량 측정 데이터의 예시를 보여주는 Figure 3과 같이, 측정값은 10~70 Pa의 압력차 범위에서 5~10 Pa 간격으로 총 10개의 데이터 포인트를 측정하고, 각 데이터 포인트당 측정시간은 120초(120s)로 설정하였다. 측정 장비는 데이터를 1초당 1개 기록하므로, 각 데이터 포인트에서 2분 동안 118~119개의 압력차와 유량 값을 얻을 수 있다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-05/N0280180502/images/Figure_KIAEBS_18_5_02_F3.jpg

Figure 3.

An example graph showing a regression line calculated from the measured airflow rates at various pressure differences

측정결과

측정 데이터

Table 2는 본 연구에 사용된 31개 감압 데이터의 n과 C_L의 평균 및 표준편차를 나타낸 것이다. OLS와 WLOC에 의해 계산된 n의 평균치는 각각 0.634와 0.627로 유효범위인 0.5~1.0을 만족한다. 한편, 누기 계수 C_L은 275.950, 283.785로 일반적인 공동주택에서 10~100의 범위로 측정(Kölsch and Walker, 2020)되는 것에 비해 상당히 크다. C_L은 누기 면적과 토출 계수(Discharge coefficient)를 곱한 값에 비례(Allard and Santamouris, 1998)하는 값으로 본 연구에서 C_L값이 큰 이유는 학교 건물이 주거용 건물과 비교하면 상대적으로 누기 면적이 크기 때문으로 판단된다. 학교 건물을 대상으로 측정한 타 연구(Kim et al; 2019; Park et al., 2020; Shim and Hong; 2023)에서 제시된 기밀성능 데이터와 비교한 결과, 본 연구의 ACH₅₀ (50 Pa 압력차에서의 공기 교환율) 평균값은 11.15로, 타 연구의 ACH₅₀의 범위인 10.95~17.8을 만족하는 것으로 확인하였다.

Table 2.

Average and standard deviation (STD) of the regression parameters for the 31 tests in depressurization, using two regression methods.

Parameter	OLS		WLOC
Parameter	Avg.	STD	Avg.	STD
n [-]	0.634	0.009	0.626	0.008
C_{_L} [-]	276.795	10.028	284.726	9.711

기밀성능 매개변수 분석결과

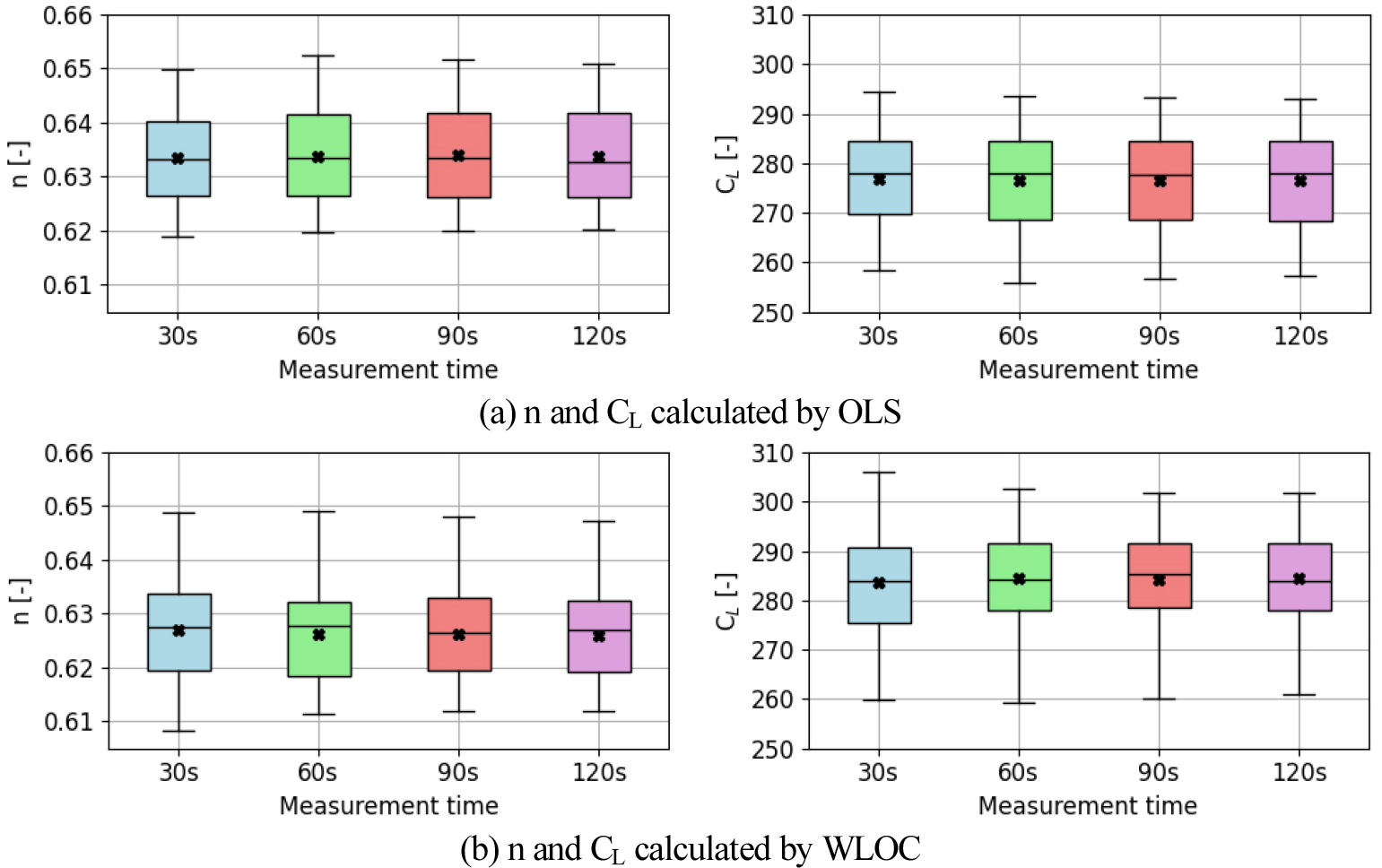
데이터 포인트 측정시간에 따른 매개변수 값 분포를 관찰하기 위해, 각 데이터 포인트에서 120s 동안 측정된 약 120개의 측정값 중 30s는 초기의 30개 측정값을 사용하였고, 60s는 60개, 90s는 90개, 120s는 120개로 데이터 포인트에서 측정된 데이터 개수를 늘려가며 계산한 n 값과 C_L값을 비교하였다. Figure 4는 31회의 측정을 대상으로, OLS (Figure 4(a))와 WLOC (Figure 4(b))를 사용하여 데이터 포인트의 측정시간별로 도출한 n과 C_L의 분포를 상자 수염 그림으로 나타낸 것이다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-05/N0280180502/images/Figure_KIAEBS_18_5_02_F4.jpg

Figure 4.

Box plot of n and C_L by OLS and WLOC, classified by measurement time

OLS를 적용하여 구한 매개변수(n, C_L)는 측정시간 증가에 따라 데이터 변동에 유의미한 변화가 없었지만, WLOC를 적용하여 구한 매개변수는 측정시간이 증가함에 따라 Whisker의 길이가 줄어드는 것을 확인할 수 있었다. Whisker는 데이터의 극단 값 범위를 나타내며, 그 길이의 감소는 극단 값의 폭이 줄어듦을 의미한다. Figure 4 데이터의 표준편차를 비교하면 Table 3과 같다. 비교의 편의를 위해 30s 데이터를 기준으로 다른 시간(60s, 90s, 120s)의 표준편차를 상대적 퍼센트(빨간색-표준편차 증가, 파란색-표준편차 감소)로 표시하였다. Table 3을 보면, OLS로 구한 매개변수의 표준편차는 측정시간 증가에 따른 변화가 없었다. 그러나 WLOC로 구한 매개변수의 표준편차는 측정시간이 60s, 90s, 120s로 증가함에 따라 n은 –11.15%, –14.00%, –15.42%로, C_L은 –12.62%, –14.62%, –16.51%로 각각 점차 감소하였다. 이는 측정시간이 늘어남에 따라 WLOC로 계산된 Figure 4(b)의 n과 C_L의 Whisker 길이뿐만 아니라, 데이터의 중간 50%를 나타내는 Box의 길이(사분위 범위, Interquartile range (IQR))도 감소함을 의미한다. 즉, WLOC는 측정시간이 증가함에 따라 데이터가 중앙값 주변에 더 밀집되어 매개변수의 분포가 좁아지는 효과가 있음을 알 수 있다.

Figure 4와 Table 3에서 OLS로 구한 매개변수가 데이터 포인트 측정시간에 영향을 받지 않는 이유는, OLS가 데이터 포인트에서 측정된 값들의 평균값만을 활용하여 회귀선을 찾기 때문이다. 따라서, 데이터 포인트 측정시간을 늘려 더 많은 데이터가 분석에 사용되더라도 데이터 포인트의 평균값이 같으면 매개변수 추정에 영향을 주지 못하는 것으로 보인다. 반면, WLOC는 각 데이터 포인트에서 측정된 값들의 평균뿐만 아니라 불확도를 반영하여, 불확도가 낮은 데이터 포인트일수록 높은 가중치를 부여해 회귀선을 찾는다. 이로 인해 반복 측정한 매개변수 간의 편차가 측정시간이 늘어남에 따라 점차 감소하는 것으로 판단된다.

Table 3.

Standard deviation of n and C_{_L} calculated by OLS and WLOC

Measurement time	Standard deviation [-]
	OLS		WLOC
	$S t d_{n}$	$S t d_{C_{L}}$	$S t d_{n}$	$S t d_{C_{L}}$
30s (baseline)	0.00859 (-)	9.913 (-)	0.00996 (-)	11.632 (-)
60s	0.00885 (+3.02%)	10.154 (+2.43%)	0.00885 (-11.15%)	10.164 (-12.62%)
90s	0.00883 (+2.77%)	10.128 (+2.17%)	0.00856 (-14.00%)	9.932 (-14.62%)
120s	0.00880 (+2.40%)	10.028 (+1.16%)	0.00842 (-15.42%)	9.711 (-16.51%)

기밀성능 매개변수의 관측 확장불확도와 계산 확장불확도 비교

앞서 WLOC로 매개변수를 구할 때 데이터 포인트 측정시간이 증가하면 반복 측정한 매개변수의 표준편차가 감소하는 것을 확인하였다. 그러나 다수의 건물 기밀성능을 평가하는 것이 목적인 경우, 반복 측정하기보다는 한 번의 기밀 측정으로 매개변수를 구하는 경우가 많다. 이 경우 관측 확장불확도로 구한 모평균 신뢰구간은 알 수 없으나 계산 확장불확도를 이용해 단일 측정값으로 모수 추정 신뢰구간을 나타낼 수 있다. 불확도는 측정값의 불확실한 정도를 나타내는 지표로, Type A 또는 Type B 평가 방법으로 구한 표준불확도를 몬테카를로 방법 또는 불확도 전파의 법칙에 따라 합성하여 구한다. 그리고 합성표준불확도에 포함인자( $k$ )를 곱하여 신뢰구간으로 표현되는 확장불확도를 구할 수 있다. 본 연구에서는 불확도 전파의 법칙(부록 B)에 따라 불확도를 합성하고, 신뢰구간 95%로( $k$ =1.96) 확장불확도를 나타냈다.

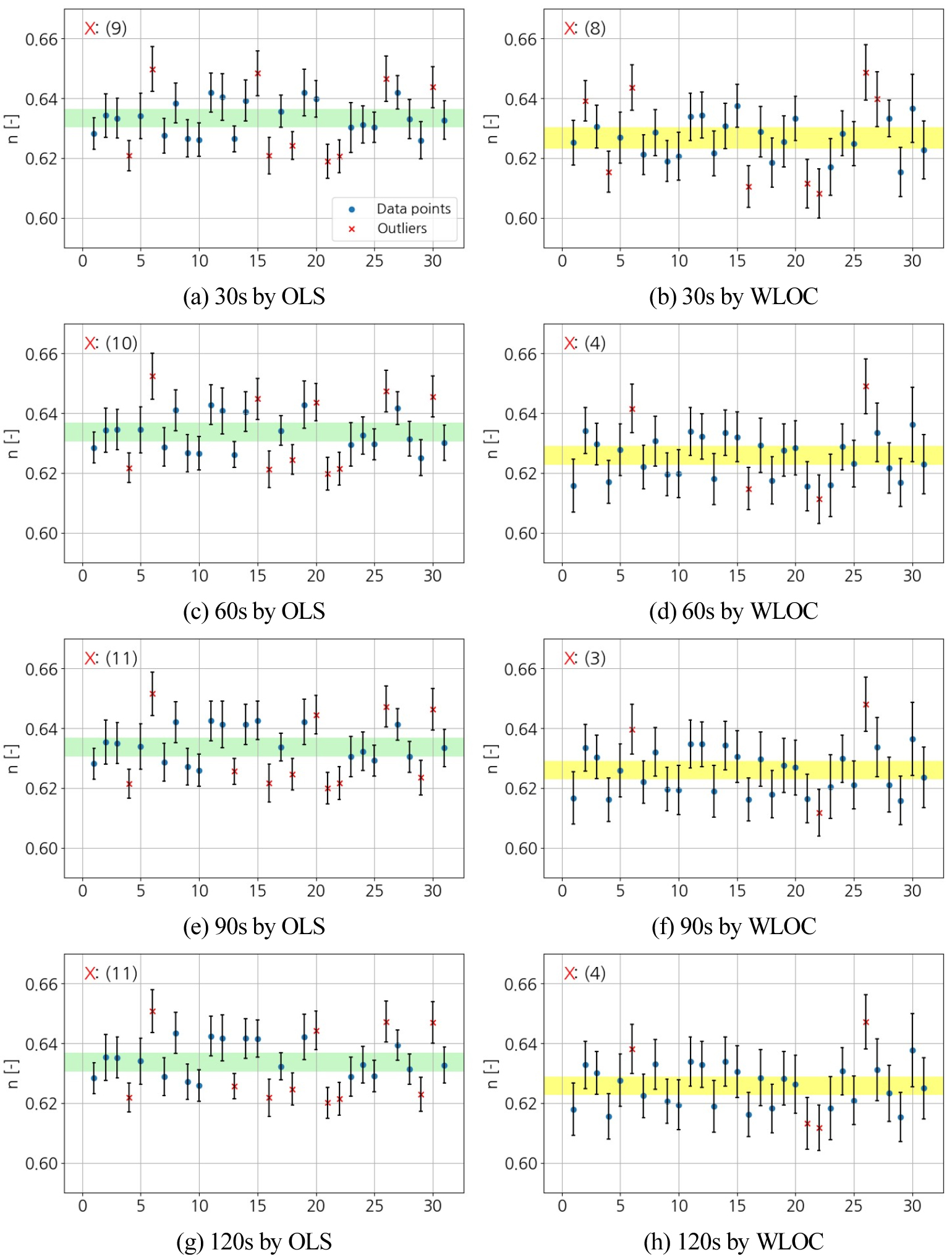
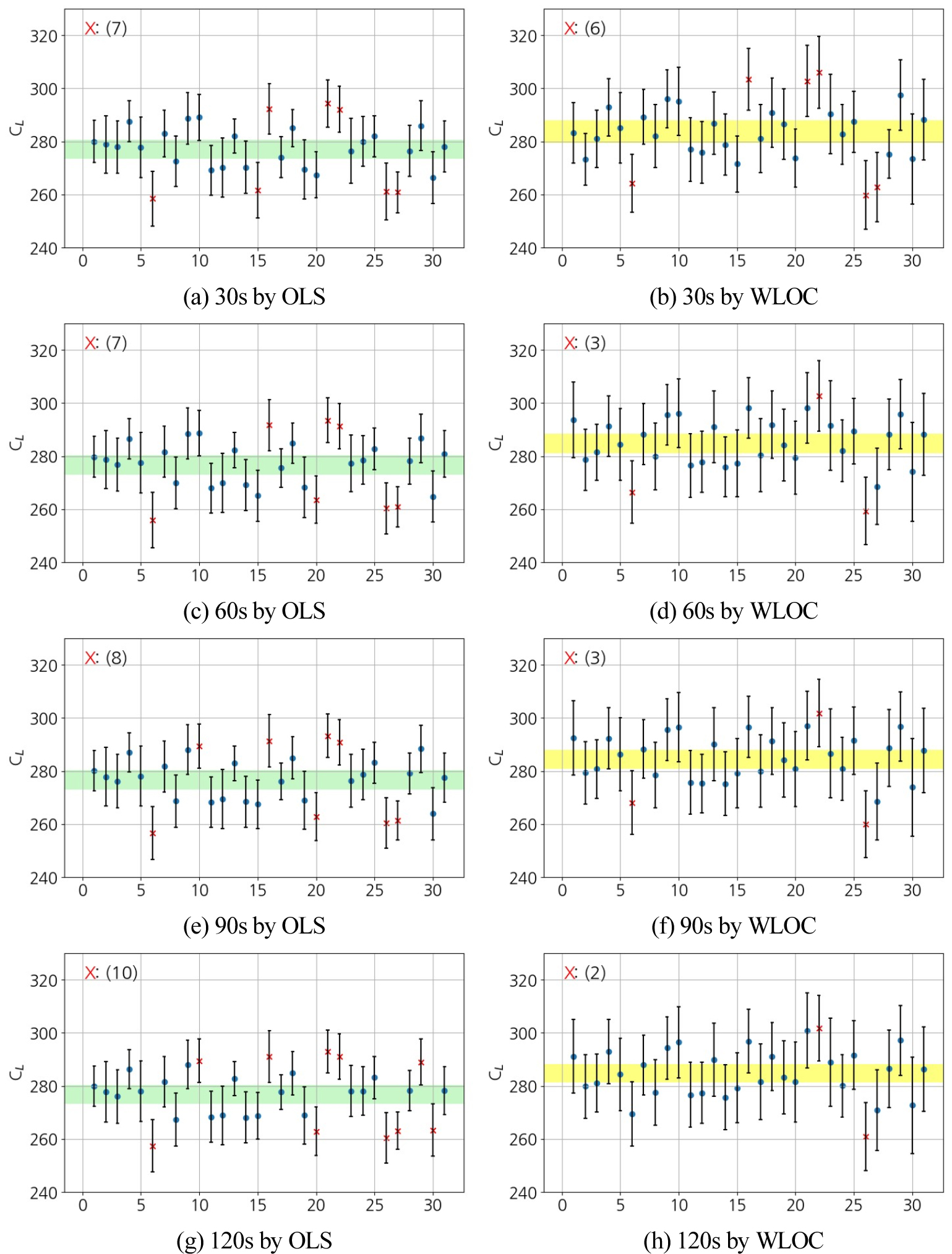
Figure 5와 6은 31회 측정에 대해 OLS와 WLOC 방법으로 각각 n과 C_L의 확장불확도를 데이터 포인트 측정시간에 따라 비교한 그래프이다. 각 그래프에서 바 차트는 31개의 개별 측정값에 대한 계산 확장불확도(모수 추정 신뢰구간)이고, 음영(초록색: OLS, 노란색: WLOC)으로 표시된 구간은 31개 전체 측정값의 관측 확장불확도(모평균 신뢰구간)를 의미한다. 31개의 바 차트 중 모평균 신뢰구간에서 벗어난 데이터(음영과 겹치는 구간이 없는 바 차트)는 ‘x’로 표시하였다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-05/N0280180502/images/Figure_KIAEBS_18_5_02_F5.jpg

Figure 5.

Comparing observed expanded uncertainty and calculated expanded uncertainty of n by OLS and WLOC

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-05/N0280180502/images/Figure_KIAEBS_18_5_02_F6.jpg

Figure 6.

Comparing observed expanded uncertainty and calculated expanded uncertainty of C_L by OLS and WLOC

그래프에 따르면, 측정시간이 30s일 때 OLS와 WLOC로 계산한 확장불확도가 관측 확장불확도 범위를 벗어나는 데이터의 수는 각각 9개와 8개로 유사하다. 그러나 측정시간이 증가함에 따라 OLS의 경우 범위를 벗어나는 데이터 수에 큰 변화가 없는 반면, WLOC는 관측 확장불확도 범위를 벗어나는 개별 계산 확장불확도 데이터 수가 감소한 것을 관찰할 수 있다. 앞서 Table 3에서, OLS의 매개변수 표준편차는 데이터 포인트 측정시간과 상관관계가 없었으나, WLOC의 표준편차는 데이터 포인트 측정시간이 증가함에 따라 감소하여 개별 측정값이 관측 확장불확도에 가까워지는 것을 확인하였다. 따라서 WLOC로 구한 매개변수 평균이 데이터 포인트 측정시간이 증가함에 따라 관측 확장불확도 범위에 근접하게 된다. Table 4는 31개의 계산 확장불확도를 평균한 후, 측정시간에 따라 나타낸 표이다. Table 4에서 WLOC의 계산 확장불확도는 측정시간이 증가함에 따라 점차 증가하는 경향이 나타난다. 이는 측정시간이 증가할수록 Figure 5와 6의 바 차트의 길이가 길어질 수 있다는 것을 시사한다. 즉, 데이터 포인트 측정시간이 증가하면 WLOC로 구한 매개변수 평균이 관측 확장불확도 영역에 근접하는 동시에 계산 확장불확도를 나타내는 바 차트의 길이가 길어지기 때문에 계산 확장불확도와 관측 확장불확도가 겹치는 구간이 늘어나게 된다.

Table 4.

Mean calculated expanded uncertainty of n and C_{_L} by OLS and WLOC

MeasurementKIAEBS_2024_185 time	Calculated expanded uncertainty [-]
	OLS		WLOC
	u_{_c}(n)	u_{_c}(C_{_L})	u_{_c}(n)	u_{_c}(C_{_L})
30s (baseline)	0.00317 (-)	4.668 (-)	0.00397 (-)	6.086 (-)
60s	0.00312 (-1.64%)	4.590 (-1.68%)	0.00421 (+6.00%)	6.483 (+6.53%)
90s	0.00308 (-2.79%)	4.537 (-2.82%)	0.00425 (+7.12%)	6.546 (+7.56%)
120s	0.00306 (-3.52%)	4.503 (-3.55%)	0.00431 (+8.56%)	6.638 (+9.08%)

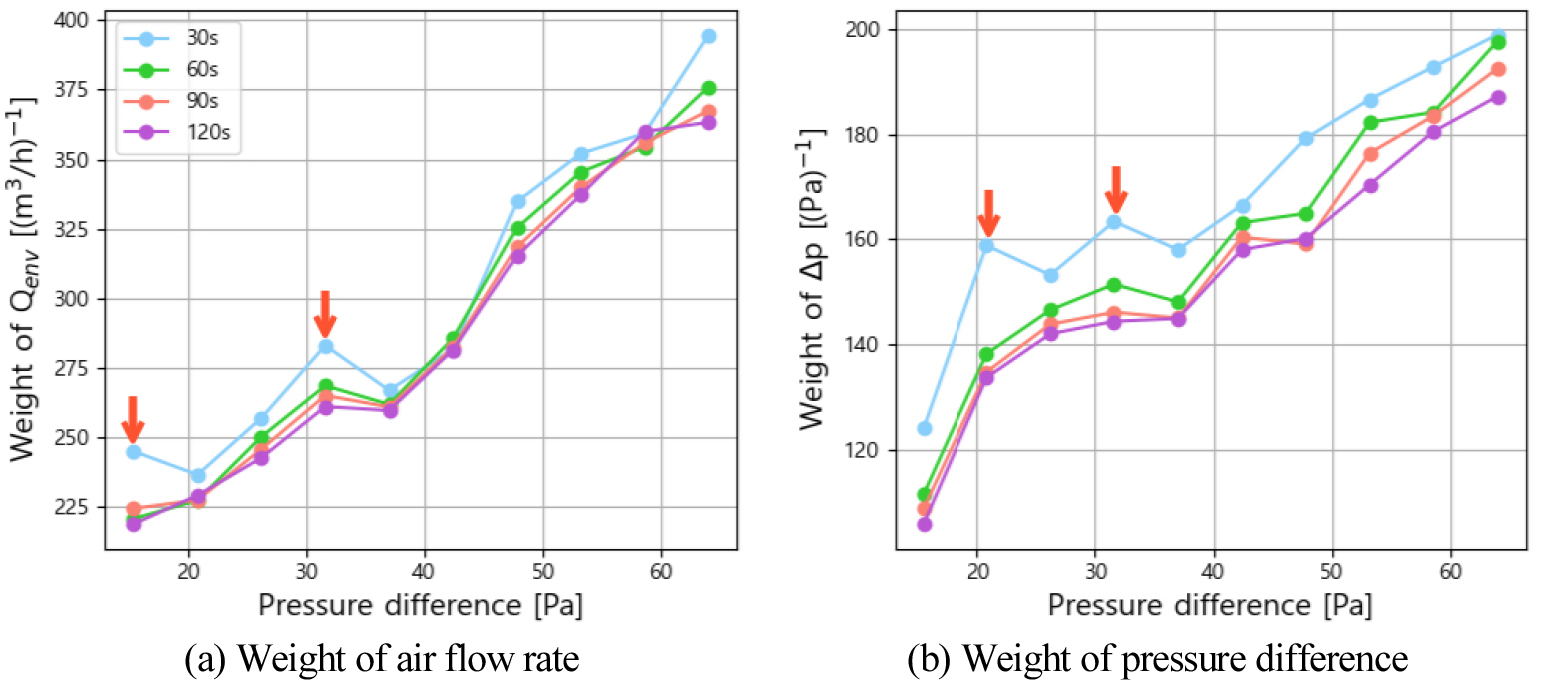
Figure 7은 31개 측정값의 각 데이터 포인트에서 고려되는 압력차와 유량의 가중치를 평균한 후, 데이터 포인트 측정시간 증가에 따라 가중치 변화를 살펴본 것이다. Figure 7의 두 그래프에서 압력차가 커질수록 데이터 포인트에서의 가중치가 증가하는 경향이 보인다. 가중치는 불확도의 역수이므로 가중치가 증가한다는 것은 불확도가 낮아진다는 것을 의미한다. 블로어도어로 형성되는 차압이 커질수록 외부풍속과 실내외 온도 차에 의해 발생하는 압력차의 영향이 적기 때문에 고압력차에서 불확도가 낮아지는 것으로 판단된다. 한편, 데이터 포인트 측정시간 증가에 따른 가중치 변화를 살펴보면, 30s에서의 가중치는 저압 구간에서 일부 가중치가 높은 것을 확인(화살표 표시 부분)할 수 있다. 저압력차 지점의 데이터 가중치가 높아지면 신뢰도가 상대적으로 낮은 데이터 포인트가 매개변수 추정에 높은 가중치로 반영되기 때문에 계산 확장불확도가 모평균 신뢰구간에서 벗어날 가능성이 크다. 그러나 데이터 포인트 측정시간을 60s로 2배 증가시키면 저압력차에서 가중치가 상승한 부분이 완화되는 것을 확인할 수 있으며, 90s와 120s로 측정시간을 더 늘렸을 때는 전반적으로 가중치가 개선되는 것을 확인할 수 있다. 또한, 앞서 Figure 5와 6에서 보듯이 데이터 포인트 측정시간을 30s에서 60s로 증가시키면 관측 확장불확도를 벗어나는 데이터가 절반으로 줄어드는 반면(n은 8개→4개, C_L은 6개→3개) 60s에서 90s, 120s로 증가하였을 때는 차이가 크지 않다(n은 4개→4개, C_L은 3개→2개). 따라서, 90s와 120s를 적용할 경우 실험 시간이 60s와 비교하면 1.5~2배 정도로 늘어나므로, 60s가 가장 효율적인 선택으로 판단된다. 본 연구결과를 종합하면, 개별 측정값으로 데이터의 신뢰구간을 나타내는 경우, WLOC 방법을 적용하여 데이터 포인트 측정시간을 60s로 하는 것이 모평균 신뢰구간을 추정하는데 효율적이라고 판단된다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2024-018-05/N0280180502/images/Figure_KIAEBS_18_5_02_F7.jpg

Figure 7.

Weight of pressure difference and airflow rate at each data point classified by measurement time

결 론

본 연구에서는 블로어도어 실험을 31회 반복 수행한 후, OLS와 WLOC 방법을 적용하여 데이터 포인트 측정시간 연장에 따른 기밀성능 매개변수의 변화를 분석하였다.

n과 C_L의 표준편차는 측정시간 증가 시 OLS에서는 감소 효과가 없었으나, WLOC에서는 60s, 90s, 120s로 늘어남에 따라 점차 감소하였다. 이는 OLS가 x축의 불확도를 무시하고 y축의 불확도를 모두 동일하게 취급하는 반면, WLOC는 각 데이터 포인트의 불확도를 반영하여 더 신뢰할 수 있는 추정치를 계산하기 때문이다. 또한, 31회의 반복 측정으로 구한 관측 확장불확도와 개별 측정값으로 구한 계산 확장불확도를 회귀방법에 따라 비교한 결과, 데이터 포인트 측정시간을 증가시켰을 때, OLS 방법은 관측 확장불확도 범위를 벗어나는 계산 확장불확도 데이터 수의 변화가 관찰되지 않았으나, WLOC 방법을 적용하면, 데이터 포인트 측정시간을 30s에서 60s로 2배 증가시켰을 때 관측 확장불확도 범위를 벗어나는 데이터 수가 절반으로 감소하였다. 이는 측정시간이 증가함에 따라 저압 구간에서 데이터 포인트에 부여되는 가중치가 고압력차 지점보다 컸던 부분이 줄어들었기 때문으로 판단된다. 다만, 60s에서 90s와 120s로 측정시간을 더 늘렸을 때 전체적으로 가중치가 개선되지만, 관측 확장불확도와 계산 확장불확도를 비교한 결과 개선되는 측정값의 수가 60s와 비교했을 때 큰 차이가 없었다. 따라서 측정시간의 효율성을 고려하면 60s가 적절해 보인다. 종합하면, 개별 측정값으로 기밀도 데이터의 신뢰도를 향상하기 위해서는 OLS 방법보다는 WLOC 방법이 적합하며, 데이터 포인트 측정시간은 30s에서 60s로 2배 증가시키는 것이 효과적이다.

Appendix A

Appendix A. 측정 조건

Table A1은 측정 기기로 기록된 실내온도, 실외온도, 외부풍속의 최솟값, 최댓값, 평균, 표준편차를 나타낸다. 총 31회의 측정은 ISO 9972의 측정 조건을 충족하는 환경에서 수행되었으며, 이는 실내외 온도 차와 건물 높이를 곱한 값(△T × height)이 250 미만이고 외부풍속이 6 m/s 미만인 조건을 말한다.

Table A1.

Maximum, minimum, average and standard deviation (STD) of weather data

Number of tests	T_{_int} [℃]				T_{_e} [℃]				v_{_wind} [m/s]
Number of tests	Max	Min	Avg.	STD	Max	Min	Avg.	STD	Max	Min	Avg.	STD
1	9.10	8.50	8.76	0.17	8.70	8.00	8.22	0.18	1.26	0.00	0.16	0.11
2	11.70	9.20	9.27	0.51	7.40	6.00	6.43	0.29	1.09	0.00	0.14	0.11
3	9.90	9.40	9.81	0.13	7.10	5.60	6.67	0.41	1.05	0.00	0.14	0.11
4	10.80	10.20	10.41	0.20	7.10	5.10	6.87	0.64	1.01	0.00	0.23	0.16
5	10.90	10.50	10.70	0.13	6.00	3.80	5.14	0.48	3.91	0.06	0.65	0.44
6	10.90	10.40	10.73	0.14	5.70	4.40	4.81	0.27	1.75	0.01	0.33	0.24
7	10.90	9.70	10.50	0.36	6.50	4.00	4.73	0.39	2.00	0.01	0.37	0.28
8	11.80	11.20	11.61	0.19	14.10	13.00	13.55	0.25	2.78	0.03	0.54	0.42
9	12.30	11.70	12.03	0.17	13.70	11.80	13.12	0.56	3.05	0.02	0.52	0.40
10	13.50	12.50	13.02	0.36	17.00	15.30	16.19	0.38	2.79	0.00	0.29	0.28
11	13.80	13.10	13.47	0.24	17.00	15.00	16.42	0.54	2.04	0.00	0.38	0.30
12	13.80	13.30	13.48	0.16	15.10	13.30	14.42	0.54	1.84	0.00	0.29	0.22
13	12.40	11.60	12.09	0.22	7.30	5.50	6.47	0.44	1.67	0.00	0.16	0.16
14	12.40	10.60	11.53	0.63	5.50	3.30	4.80	0.63	1.67	0.00	0.17	0.12
15	11.90	11.20	11.55	0.22	8.20	6.40	7.77	0.54	1.72	0.01	0.27	0.18
16	11.70	10.80	11.29	0.26	6.20	5.10	5.83	0.34	1.49	0.01	0.25	0.17
17	11.50	10.50	11.07	0.28	5.00	3.80	4.57	0.34	1.70	0.01	0.26	0.18
18	11.80	10.90	11.28	0.22	8.40	5.10	5.88	0.71	2.26	0.00	0.31	0.24
19	12.10	11.60	11.92	0.14	9.00	7.60	8.19	0.32	2.17	0.00	0.30	0.25
20	12.20	11.80	12.04	0.09	9.70	8.20	8.97	0.34	1.83	0.00	0.26	0.21
21	12.00	11.30	11.71	0.22	7.90	6.80	7.66	0.35	1.82	0.00	0.11	0.14
22	12.10	11.20	11.78	0.30	7.50	6.10	7.02	0.40	0.80	0.00	0.15	0.11
23	12.50	11.50	11.94	0.25	11.20	7.50	8.84	0.75	1.55	0.00	0.28	0.22
24	12.90	12.10	12.60	0.17	12.50	9.70	10.90	0.62	2.60	0.00	0.36	0.33
25	13.60	12.70	13.06	0.22	11.40	9.70	10.74	0.45	1.98	0.00	0.42	0.31
26	13.30	12.30	12.75	0.27	9.50	8.30	9.15	0.33	1.91	0.01	0.31	0.25
27	13.20	12.80	12.89	0.10	8.50	7.00	8.04	0.33	1.62	0.01	0.32	0.25
28	12.90	12.10	12.51	0.20	9.70	7.50	8.43	0.44	1.64	0.00	0.19	0.17
29	13.30	12.70	12.92	0.17	11.40	9.30	10.28	0.47	1.21	0.01	0.18	0.13
30	13.80	13.40	13.65	0.12	11.50	9.90	10.84	0.43	1.11	0.00	0.16	0.14
31	14.00	12.60	13.26	0.47	10.20	7.60	9.24	0.69	2.28	0.01	0.33	0.24

Appendix B

Appendix B. 합성표준불확도(Combined standard uncertainty)

불확도 전파의 법칙(The law of propagation of uncertainty)

측정결과 값 y의 표준불확도는 그 결과가 관계함수(ƒ)를 통해 여러 입력값 x_i에서 얻어진 경우, 합성표준불확도라고 하며 u_c(y)로 표시한다. 입력값에 대한 합성표준불확도는 불확도 전파의 법칙에 따라 각 입력값의 불확도와 공분산을 고려하여 계산한다. 입력값 간 상관관계가 없는 경우와 있는 경우는 각각 식 (1), (2)에 의해 계산할 수 있다. 여기서, 입력값 x_i의 불확도는 u(x_i), N은 입력값의 개수, r(x_i, x_j)는 입력값 x_i와 x_j의 상관계수이다.

(1)

u_{c} (y) = \sqrt{\sum_{i = 1}^{N} {(\frac{\partial f}{\partial x_{i}} u (x_{i}))}^{2}}

(2)

u_{c} (y) = \sqrt{\sum_{i = 1}^{N} {(\frac{\partial f}{\partial x_{i}} u (x_{i}))}^{2} + 2 \sum_{i = 1}^{N - 1} \sum_{j = i + 1}^{N} (\frac{\partial f}{\partial x_{i}}) (\frac{\partial f}{\partial x_{j}}) u (x_{i}) u (x_{j}) r (x_{i}, x_{j})}

기밀성능 매개변수의 합성표준불확도 계산

C_L의 합성표준불확도는 불확도 전파의 법칙에 따라 식 (3)로 계산할 수 있다(Delmotte, 2013). 여기서 T_o는 표준온도 293.15 K를 의미하며, T_e는 실외온도를 의미한다. u_c(a), u_c(b), r(a, b)는 Table B1와 같이 회귀방법에 따라 계산방법을 다르게 적용한다.

(3)

\begin{aligned} u_{c} (C_{L}) = \sqrt{\begin{matrix} {(e^{b} {(\frac{T_{o}}{T_{e}})}^{1 - a} \ln (\frac{T_{e}}{T_{o}}) u_{c} (a))}^{2} + {(e^{b} {(\frac{T_{o}}{T_{e}})}^{1 - a} u_{c} (b))}^{2} \\ + {(\frac{e^{b} (a - 1)}{T_{e}} {(\frac{T_{o}}{T_{e}})}^{1 - a} u_{c} (T_{e}))}^{2} \\ + 2 {(e^{b} {(\frac{T_{o}}{T_{e}})}^{1 - a})}^{2} \ln (\frac{T_{e}}{T_{o}}) u_{c} (a) u_{c} (b) r (a, b) \end{matrix}} \end{aligned}

Table B1.

Equations of combined standard uncertainty (Delmotte, 2013; Delmotte, 2017)

uncertainty	OLS	WLOC
$u_{c} (a) =$	$\sqrt{\frac{\frac{\sum (y_{i} - y_{i, e s t i m a t e d})^{2}}{n - 2}}{n \sum x_{i}^{2} - (\sum x_{i})^{2}}}$	$\sqrt{\sum ({(\frac{\partial a}{\partial x_{i}})}^{2} \frac{1}{v_{i}^{2}} + {(\frac{\partial a}{\partial y_{i}})}^{2} \frac{1}{w_{i}^{2}})}$
$u_{c} (b) =$	$u_{c} (a) ∙ \sqrt{\frac{\sum x_{i}^{2}}{n}}$	$\sqrt{\sum ({(\frac{\partial b}{\partial x_{i}})}^{2} \frac{1}{v_{i}^{2}} + {(\frac{\partial b}{\partial y_{i}})}^{2} \frac{1}{w_{i}^{2}})}$
$r (a, b) =$	$- \frac{\sum x_{i}}{\sqrt{N \sum x_{i}^{2}}}$	$\frac{u_{c}^{2} (a + b) - u_{c}^{2} (a) - u_{c}^{2} (b)}{2 u_{c} (a) u_{c} (b)}$

여기서,

$\frac{\partial b}{\partial x_{i}} = \frac{\sqrt{∆ y}}{\sqrt{∆ x}} (\frac{- v_{i} w_{i}}{\sum v_{i} w_{i}} - \frac{(\sum v_{j} w_{j} x_{j})^{2} v_{i} w_{i}}{∆ x \sum v_{j} w_{j}} + \frac{(\sum v_{j} w_{j} x_{j}) v_{i} w_{i} x_{i}}{∆ x})$ ,

$\frac{\partial b}{\partial y_{i}} = \frac{v_{i} w_{i}}{\sum v_{j} w_{j}} - \frac{(\sum v_{j} w_{j} x_{j}) v_{i} w_{i} y_{i}}{\sqrt{∆ x} \sqrt{y}} + \frac{(\sum v_{j} w_{j} x_{j}) (\sum v_{j} w_{j} y_{j}) v_{i} w_{i}}{\sum v_{j} w_{j} \sqrt{∆ x} \sqrt{∆ y}}$ ,

$\frac{\partial a}{\partial x_{i}} = \frac{\sqrt{∆ y}}{\sqrt{∆ x}} \frac{((\sum v_{j} w_{j} x_{j}) v_{i} w_{i} - (\sum v_{j} w_{j}) v_{i} w_{i} x_{i})}{∆ x}$ ,

$\frac{\partial a}{\partial y_{i}} = \frac{\sqrt{∆ y}}{\sqrt{∆ x}} \frac{((\sum v_{j} w_{j}) v_{i} w_{i} y_{i} - (\sum v_{j} w_{j} y_{i}) v_{i} w_{i})}{∆ y}$ ,

$\sqrt{\frac{∆ y}{∆ x}} = \frac{\sqrt{\sum v_{i} w_{i} \sum v_{i} w_{i} y_{i}^{2} - (\sum v_{i} w_{i} y_{i})^{2}}}{\sqrt{\sum v_{i} w_{i} \sum v_{i} w_{i} x_{i}^{2} - (\sum v_{i} w_{i} x_{i})^{2}}}$

Acknowledgements

이 논문은 2024년도 광운대학교 교내학술 연구비 지원에 의해 연구되었음.

References

Choi, J.S., Ji, K.H., Lee, D.S., Jo, J.H. (2014). A study on uncertainty experiment depending on testers in airtightness measurement of buildings. Journal of KIABES, 8(2), 40-45.

Kim, J.H., Hwang, I.T., Park, J.H. (2022). Comparison of building airtightness based on regression techniques (Ordinary Least Square vs. Weighted Line of Organic Correlation). Journal of KIAEBS, 16(5), 333-345.

Kölsch, B., Walker, I.S. (2020). Improving air leakage prediction of buildings using the fan pressurization method with the Weighted Line of Organic Correlation. Building and Environment, 181, 107157.

10.1016/j.buildenv.2020.107157

Mélois, A., Carrié, F.R., El Mankibi, M., Moujalled, B. (2022). Uncertainty in building fan pressurization tests: Review and gaps in research. Journal of Building Engineering, 52, 104455.

10.1016/j.jobe.2022.104455

Okuyama, H., Onishi, Y. (2012). Reconsideration of parameter estimation and reliability evaluation methods for building airtightness measurement using fan pressurization. Building and Environment, 47, 373-384.

10.1016/j.buildenv.2011.06.027

Park, H.C., Lee, J.Y., Yee, J.J. (2020). A study on the measurement of air-tightness performance and measures to prevent fine dust inflow of school classrooms. Journal of the Architectural Institute of Korea, 36(8), 101-106.

Prignon, M., Dawans, A., Altomonte, S., Van Moeseke, G. (2019). A method to quantify uncertainties in airtightness measurements: Zero-flow and envelope pressure. Energy and Buildings, 188, 12-24.

10.1016/j.enbuild.2019.02.006

Prignon, M., Delmotte, C., Dawans, A., Altomonte, S., van Moeseke, G. (2020). On the impact of regression technique to airtightness measurements uncertainties. Energy and Buildings, 215, 109919.

10.1016/j.enbuild.2020.109919

Shim, C., Hong, G. (2023). Airtightness Assessment under Several Low-Pressure Differences in Non-Residential Buildings. Energies, 16(19), 6845.

10.3390/en16196845

Delmotte, C. (2013). Airtightness of buildings - Calculation of combined standard uncertainty. Proceedings of the 34th AIVC Conference, Athens, Greece, 25-26.

Delmotte, C. (2017). Airtightness of buildings - Considerations regarding the zero-flow pressure and the weighted line of organic correlation. Proceedings of the 38th AIVC Conference, Nottingham, UK, 13-14.

Kim, D.H., Lee, S.J., Jeong, C.H., Yeo, M.S., Ryu, S.R. (2019). Performance analysis of insulation and airtightness for school buildings in winter and summer seasons by field measurement. Proceedings of the 2019 Winter Conference of the Society of Air-Conditioning and Refrigerating Engineers of Korea, 318-321.

Hurel, N., Leprince, V. (2021). Impact of wind on the airtightness test results. AIVC Ventilation Information Paper, 41.

Allard, F., Santamouris, M. (1998). Natural ventilation in buildings: A design handbook. James & James (Science Publishers) Ltd.

ISO 9972. (2015). Thermal performance of buildings-Determination of air permeability of buildings-Fan pressurization method.

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems ISSN:1976-6483(Print) 2586-0666(Online) 한국건축친환경설비학회논문집

Preview

Analysis of the Impact of Extended Data Point Measurement Time on Uncertainty in the Blower Door Test

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Figure 1.

Photo and floor plan of test room

Table 1.

Summary of measurement site

Figure 2.

Installation of measurement equipment and test environment

Figure 3.

An example graph showing a regression line calculated from the measured airflow rates at various pressure differences

Table 2.

Average and standard deviation (STD) of the regression parameters for the 31 tests in depressurization, using two regression methods.

Figure 4.

Box plot of n and CL by OLS and WLOC, classified by measurement time

Table 3.

Standard deviation of n and CL calculated by OLS and WLOC

Figure 5.

Comparing observed expanded uncertainty and calculated expanded uncertainty of n by OLS and WLOC

Figure 6.

Comparing observed expanded uncertainty and calculated expanded uncertainty of CL by OLS and WLOC

Table 4.

Mean calculated expanded uncertainty of n and CL by OLS and WLOC

Figure 7.

Weight of pressure difference and airflow rate at each data point classified by measurement time

Appendix A

Table A1.

Maximum, minimum, average and standard deviation (STD) of weather data

Appendix B

(1)

(2)

(3)

Table B1.

Equations of combined standard uncertainty (Delmotte, 2013; Delmotte, 2017)

Acknowledgements

References

Box plot of n and C_L by OLS and WLOC, classified by measurement time

Standard deviation of n and C_{_L} calculated by OLS and WLOC

Comparing observed expanded uncertainty and calculated expanded uncertainty of C_L by OLS and WLOC

Mean calculated expanded uncertainty of n and C_{_L} by OLS and WLOC