서 론

실내 온열환경은 차양장치, 냉난방 공조시스템, 복사 냉난방 시스템 등 다양한 유형의 냉난방 시스템을 통해 제어된다. 이러한 냉난방 시스템의 제어는 실내 온열환경 정보를 기반으로 제어된다. 실내 온열환경을 조성하는 다양한 물리적 인자로는 공기온도, 습도, 평균복사온도(Mean Radiant Temperature, MRT), 기류속도 등이 있다. 이중 MRT는 실제로는 인체와 실내표면 간의 복잡한 복사 열교환의 영향을 가상의 균일한 표면온도로 이루어진 흑체 내부에서의 복사열 교환의 영향으로 변수화 한 것을 의미한다. MRT는 이를 온도 단위(K 또는 °C)로 표현한다(Halawa et al., 2014). MRT는 재실자가 경험하는 온열 환경의 절반 정도의 영향을 가진다고 보고된 바 있다(Guo et al., 2020). 기존의 MRT 측정 방법으로는 흑구온도(Marino et al., 2017), 열화상 카메라(Zampetti et al., 2018), 장파 및 단파 복사계(Walikewitz et al., 2015), 접촉식 온도센서(Wang et al., 2019) 등을 활용하는 다양한 방법들이 사용되어왔다. 이러한 방법들은 준비된 실험 공간 내에 장비를 설치하여 단기간 측정하는 방법으로, 장파 및 단파장 복사열교환의 영향을 분석하고 이를 통한 종합적인 온열환경의 평가, 효과적인 복사 난방 제어의 가능성을 보여주었다.

실제 운영중인 건물에서 온열환경을 측정하고 이를 기반으로 냉난방 설비를 제어하기 위해서는 결국 물리 센서가 설치되고 이를 기반으로 모니터링 되어야 한다. 대표적인 측정방법인 흑구 온도계나 장단파복사계를 이용한 방법들은 측정 대상이 되는 위치에 센서를 직접 설치해서 평균복사온도를 측정한다. 이러한 방법들은 실제 재실자가 사용하는 공간에 센서를 설치해야 하므로 재실자의 활동 공간 침해, 동선 방해 등의 물리적 한계가 있다.

이를 보완하기 위한 방법으로 주변의 물리적인 영향들을 측정한 후 측정 대상으로 하는 위치에서의 MRT를 계산하는 방법이 적용될 수 있다. 대표적으로는 열화상 카메라(Zampetti et al., 2018) 또는 접촉식 온도 센서(Wang et al., 2019) 등이 주로 활용되어왔다. 이중 열화상 카메라는 원격으로 표면온도를 측정할 수 있기 때문에 센서 설치 위치의 자율성을 보장할 수 있다. 열화상 카메라는 정확한 표면온도의 측정이 필요한데 이를 위해서는 방사, 반사, 대기 보상의 보정 과정이 추가적으로 필요하다(Lee et al., 2020). 보정 과정은 표면온도 측정 후에 이루어지는 작업으로 숙련된 전문가의 기술이 필요하다. 소요 비용 역시 열화상 카메라의 실질적인 건물 적용에 대한 한계점으로 인식된다(Sung et al., 2023). 최근 저가형 열화상 카메라가 많이 보급되고 있음에도 불구하고 기존의 건물에 적용되는 온열 환경 센서들을 고려했을 때 상대적으로 고가이며 비용적인 측면에서 한계가 있다.

이로 인하여 운영 중인 건물에서 연속적으로 MRT를 모니터링하는 것은 어렵고, 한 시점에서의 MRT 값을 도출하거나 실험 단계에서 이를 적용한 연구 사례들이 제시되었다. 따라서 운영 중인 건물에서 실시간으로 MRT를 측정하기 위해서는 재실자의 활동 공간 확보, 센서 비용 최소화를 위한 방법이 요구된다.

본 연구에서는 실제 건물에 적용가능한 MRT 평가 방법 개발을 위해 MRT를 예측하는 방법을 제안하였다. 앞서 언급한 재실자의 활동 공간 확보를 위해 가상센싱 알고리즘을 도입하였다. 또한 센서 비용의 최소화를 위해 추가 센서의 설치 없이 기존 센서와 공공 데이터를 활용하는 가상센서 알고리즘을 개발하였다. 평균복사온도 예측 실험을 위해 대구 지역 대학 내 강의실을 선정하였으며 동절기 3일 간 실험을 진행하였다. 표면온도 측정을 위한 방법은 기존 연구에서 개발된 Pan-tilt IR Scanning system (i.e. IR system) (Lee and Jo, 2021b)을 활용하였다. 건물 정보를 고려한 RC (Resistance and Capacity) 모델을 제안하고, particle swarm optimization (PSO) 최적화 모델을 사용하여 R, C값의 최적 해를 도출하여 표면온도 예측 알고리즘을 개발했다. 기존의 IR system을 사용한 MRT 측정 결과와 가상센싱 알고리즘을 활용한 MRT 예측 결과를 비교 검토하고, 향후 건물에서의 활용방안에 대해 논의하였다.

Figure 1.

Differences in proposed method for MRT considering longwave (LW) – shortwave (SW) radiation

MRT 예측 모델 개발

연구 프로세스

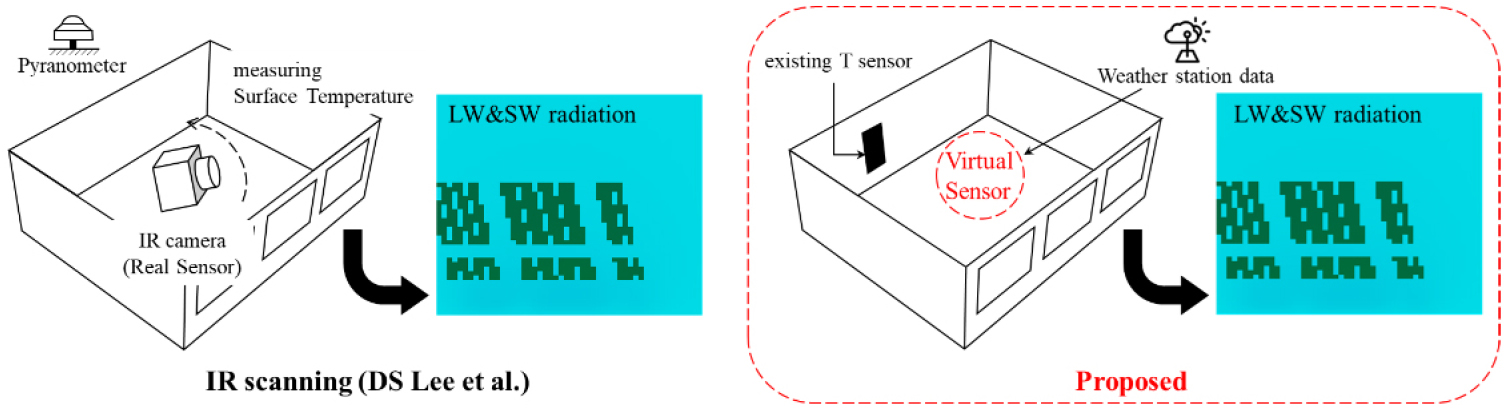
MRT 예측 모델 도출을 위해 두 가지 방법으로 MRT 계산을 진행하였다(Figure 1 참조). 제안하는 방법의 검토를 위해 동절기 3일 간 실내 표면온도 실측 실험을 진행하였다. 실내 표면온도 데이터 (TSj,mea.)는 기존 연구에서 개발된 IR system을 적용하여 취득한다. 기상청에서 제공하는 공공 데이터인 수평면 전일사량(Ig), 외부 온도(To), 그리고 기존 건물에 존재하는 공기 온도 센서를 이용한 실내 온도(Trm)를 사용하였다. Ig는 직산분리 모델(Decomposition model) (Lee and Kim, 2018)을 적용하여 직달 일사(Idir)와 확산 일사(Idif)를 분리하였다. TSj,mea., Idir, Idif 값을 각각 MRT 계산 식에 대입해 MRT를 도출하였다. 아래 Figure 2는 가상센싱 알고리즘을 활용한 MRT 예측 모델의 개발 과정이다.

Figure 2.

Derivation process of Virtual Sensor

표면온도 예측 알고리즘의 개발을 위해, 첫째 날 하루 동안 10분 간격으로 측정된 데이터를 사용하였다. RC 모델과 PSO 최적화 과정을 거쳐 R, C값의 최적 해를 찾아 표면온도 예측 모델을 도출하였다. 도출된 예측 모델에 남은 이틀 간의 Ig, To, 그리고 Trm 값을 입력하여 TSj,est. 데이터를 예측하였다. 그리고 MRT 계산모델에 입력변수로 사용하여 이틀 동안의 MRT 값을 예측하였다. 마지막으로 실측 실험을 통해 계산된 MRT 값과의 비교 검토 과정을 진행하였다.

실측 실험

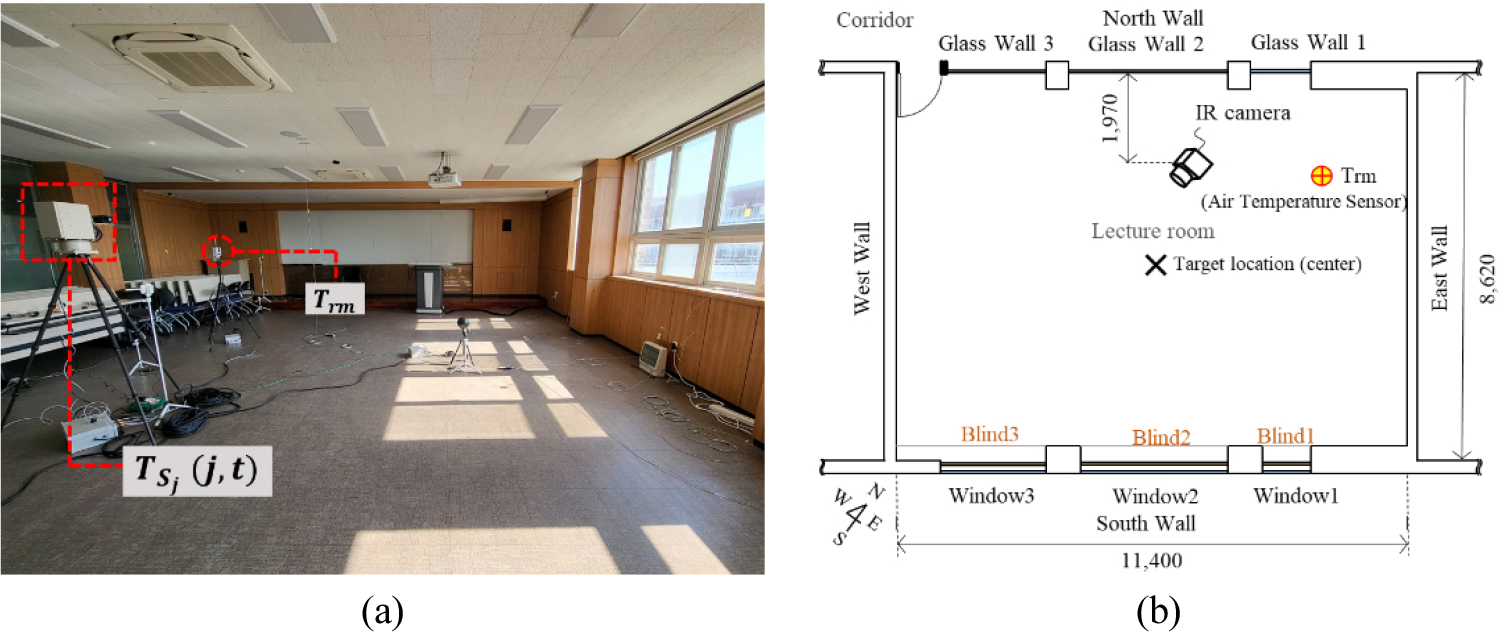
MRT 예측 모델 개발에 관한 연구를 진행하기 위해 실내 표면온도 실측 실험을 진행하였다. 실험 공간은 대구 소재 대학교 내 강의실을 선정하였다. 동절기 3일 간 실측 실험을 수행하였으며, 실험에 사용된 장비 세팅은 Figure 3와 같다. 실내 표면온도 측정을 위해서 기존 연구에서 개발된 IR system을 이용하여 데이터를 수집하였다.

Figure 3.

Experimental setup: (a) measuring instruments, (b) installation locations

MRT를 계산하기 위한 식은 다음의 식 (1)을 사용하여 계산된다. TSj,mea.4(i,t)는 시간 t에 따른 실내 표면 j의 표면온도이다. Idif'⊢(j',t)는 시간 t에 따른 유리 표면 j'를 통과해 입사되는 확산일사량이다. I'DN(i,t)는 유리를 통과하여 시간 t에 따른 재실자 위치 i로 입사되는 직달일사량이다. 여기서 유리를 통해 통과되는 일사량은 유리의 일사 투과율(Solar transmittance)에 의해서 결정된다. 일사투과율은 대상 건물 유리창의 정보를 WINDOW 6 프로그램에 입력하여 창 모델링을 통해 1차적으로 도출되었고, 실측 값을 통해서 실제 대상 외피에 맞도록 보정되었다. 마지막으로 입사각에 따른 선형 일사투과율 예측식으로 도출하였다(Lee and Jo, 2021a). Fi-j는 재실자의 위치 i와 모든 실내 표면 j사이의 형상계수이다. fproj는 인체 투영 면적에 대한 비율로, 직달일사가 인체 표면에 입사되는 면적을 전체 인체 표면적으로 나눈 값으로 계산된다. 이는 태양의 고도와 재실자의 전면 방향을 기준으로 한 태양의 위치 방위각에 따른 변수이다(Kántor and Unger, 2011). 그리고 αk는 단파복사 흡수계수로 0.57로 설정하였고(Lee and Jo, 2022), σ는 Stefan-Boltzmann 상수로 5.67×10-8[Wm-2K-4] 값을 갖는다. εP는 재실자의 방사율을 뜻하며 0.97로 설정했다(Lee and Jo, 2022). 여기서 형상계수를 비롯한 나머지 인자들은 상수로, 한번의 계산 또는 설정을 통해 건물 운영기간동안 영구적으로 사용 가능하다. 실내 모니터링을 위해서 반복적으로 측정해야 하는 인자들은 표면온도, 직달 및 확산일사가 된다.

실내 표면온도 측정을 위해 IR system으로 측정한 실내 표면온도의 값은 Figure 4와 같다. 표면은 바닥(Floor), 천장(Ceiling), 벽(East, West, South, North wall), 유리벽(Glass wall 1, 2, 3), 창문(Window 1, 2, 3)으로 나누어 12개 표면의 온도를 측정하였다. Figure 4는 실내 모든 표면에 대하여 3일간 10분 간격으로 측정된 결과를 나타낸다. 측정결과는 창표면을 제외한 9개의 표면 영역에서 약 2°C 내외의 온도차를 갖는 것으로 나타났다(Figure 4의 a 부분 참조). 창표면의 경우 낮과 밤의 온도 편차가 최고 10°C 이상 차이가 나타남을 확인할 수 있었다. 창표면 간 가장 온도차가 크게 나타나는 범위는 낮 11시 부분으로 약 2°C 내외의 표면온도 차이를 보였다(Figure 4의 b 부분 참조).

Figure 4.

Surface Temperatures measured by IR system

본 연구에서는 RC 모델을 이용하여 표면온도 예측 모델을 작성하고자 하였다. RC모델 특성상 입력 변수가 제한적일 때, 병렬구조의 R 레이어가 많아질수록 PSO 모델을 통한 R, C 값의 최적해 도출이 어려워진다. 이에 복잡한 모델 구성을 피하는 방법을 택하고, 유사 온도범위를 갖는 표면들의 그룹화를 통한 모델 단순화 방법을 제안하였다. Figure 4에 나타난 표면온도의 변화곡선과 범위를 살펴보면 크게 벽과 창문으로 나눌 수 있다(즉, Figure 4a 및 b). 그룹 내 표면 간 온도의 차이가 발생하지만, 정확한 표면온도 측정 후 식 (1)의 첫번째 항에서 보면 알 수 있듯이 그룹 내 편차는 재실자 위치에서의 형상계수(Fi-j)가 반영될 때, 도출되는 MRT 값에 미치는 영향은 낮아진다. Figure 5는 9개 벽 표면온도 평균과 3개 창문 표면온도 평균을 도출하여 2 개의 단순화된 실내 표면온도에 대한 3일간의 온도변화 값을 나타낸다.

Figure 5.

Derived surface temperature (Twd,Twl)

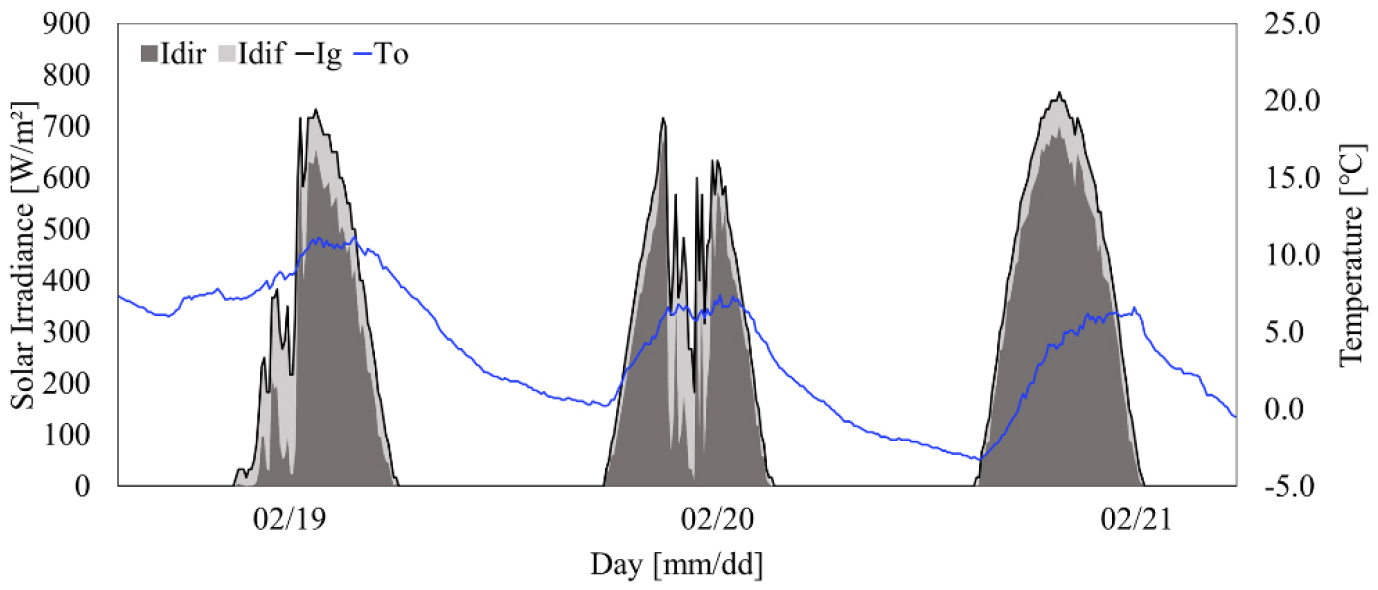
앞서 식 (1)의 2, 3항은 일사에 의한 단파복사 MRT 열전달 영향을 보여준다. 이 과정에서 직달일사와 확산일사는 서로 다른 형태로 인체표면과 열교환을 한다. 기상청 제공 일사량은 전일사(Ig)만을 제공하므로, 이를 직산분리모델을 사용해서 성분 분리를 진행하였다. 직산분리 모델은 복잡한 계산 과정을 거치지만, 실시간 전일사와 시간별 태양고도각 데이터를 이용하면 분리된 직달 및 확산일사의 모니터링이 가능하다. 실제 창호면을 투과하여 입사되는 직달 및 확산일사는 경사면 일조량 변환모델과 설치된 창호의 일사투과율(solar transmittance) 값을 이용하여 계산이 가능하다. 기상청 및 직산분리모델을 통해 도출된 Ig,Idir 및 Idif의 결과와 To는 Figure 6와 같다.

Figure 6.

Derived global, diffuse, and direct irradiance on horizontal plan, and outdoor temperature (To)

MRT 예측 모델 도출

RC 모델은 집중 매개변수로, 실내의 공기온도에 영향을 미치는 외피의 열 성능, 실내 열 취득, 실외 기온 및 일사 등 다양한 열적 매개변수를 고려하여 개발한다(Kwon et al., 2021). 대상 공간에 대한 건물 모델 정보와 MRT 예측에 필요한 최소 인자를 고려하여 3R2C로 정의된 RC 모델을 제안하였다. 여기서 투과된 일사는 복사이므로 복사의 영향을 받는 벽체에 직접 영향을 줄 수 있도록 RC 모델을 작성하였다. 여기서 R은 열저항을 나타내는 것으로, 건물의 외피면적을 함께 고려한 저항 값이다. 그리고 이때 열이 흡수되는 정도를 표현하기 위해 흡수율을 적용하였다. Figure 7은 제안된 모델을 도식화하여 나타낸 것이다.

Figure 7.

Schematic diagram of 3R2C model

여기서 Trm은 실내 공기 온도, To는 외부 온도로 기존 공기온도 센서와 기상청 공공 데이터에서 얻어 사용하는 input값이다. 그리고 Twl과 Twd는 각각 벽체 온도와 창문 온도이며, 도출된 가상센서 알고리즘을 통해 예측되는 값이다. 일사에 의한 영향은 입사일사량(Qsol)과 열전달계수(αsol)을 사용하였다.

복사 열전달은 공기온도에 직접 영향을 주지 않는다. 그러므로 일사에 의해 전달되는 모든 형태의 복사는 벽체와 창호에 전달되는 것으로 작성하였다. 벽체와 창호간 복사열전달은 모델 단순화를 위해 대류에 의해 전달되는 것으로 가정하였다. 침기에 의한 영향은 실내외 압력차가 큰 공간에서는 매우 큰 영향을 미치지만, 공조를 하지 않는 저층 건물에서 개발 모델의 단순화를 위해서 생략하였다.

PSO 최적화 모델을 사용하여 3R2C 모델에서 미지의 매개변수인 3개의 R값과 2개의 C값을 도출하였다. 모델은 MATLAB (MathWorks, 2024)을 통해 사용하였다. 사용한 RC모델의 행렬식은 다음 식 (2)와 같다. 여기서 T˙wd, T˙wl은 각각 Twd, Twl의 시간에 대한 미분항이다.

앞서 얻은 실측 표면온도, 수평면 전일사량, 실내외 온도 데이터를 이용하여 표면온도 예측 모델로 표면온도를 도출하였다. 도출한 표면온도 데이터는 Figure 8과 같다.

Figure 8.

Derived window temperature (Twd) and wall temperature (Twl) by surface temperature (TSj,est.) Estimation Model

예측된 표면 온도는 오차 발생 구간이 1시간 정도이며 최대 오차는 5.4°C 까지 나타난 것을 확인하였다. 이는 단순화된 RC 모델의 한계인 것으로 보이며 추후 상세한 모델링을 통해 개선이 필요할 것으로 판단된다. MRT 계산 식 (1)의 첫번째 항에 있는 형상계수를 반영한다면 MRT 값의 오차범위가 줄어들 것으로 판단된다.

모델 검토

앞서 단순화한 표면온도 데이터로 MRT를 계산한 것과 RC 모델을 통해 예측한 표면온도 데이터로 MRT를 계산한 것을 비교 검토하였다. Figure 9(a)는 중앙 점에서의 실험을 통해 측정된 MRT와 가상센서 알고리즘을 통해 예측된 MRT를 비교하는 그래프이다. 비교를 위해 10분 간격으로 MRT를 도출했다. Figure 9(b)에서 측정된 MRT와 예측된 MRT의 결과 값의 오차를 비교했을 때 가장 오차가 큰 부분의 값이 0.9977°C 로, 전체적으로 ± 1°C 이내의 오차를 보이고 있다.

Figure 9.

Compared Measured and Estimated MRT at center point: (a) shows estimated MRT with measured MRT. (b) shows errors by two ways (MRTmea.-MRTest.)

Figure 10.

Measured and estimated longwave and shortwave MRTs (2023.02.21.)

Figure 10은 도출된 결과를 바탕으로 대상 공간 내 MRT의 분포를 나타낸 것이다. 실물 센서와 가상 센서로 도출한 MRT 결과 값 중 2월 21일 9시 5분의 결과를 비교하였다. a는 IR system을 이용한 실물 센서의 결과를 나타낸 것이고, b는 표면온도 예측 모델을 이용한 가상 센서의 결과를 나타낸 것이다. [A]점을 비교해보면 a 에서의 MRT는 15.8°C로 나타났고, b 에서의 MRT는 15.5°C로 나타났다. 또한 [B]점을 비교했을 때 a 에서의 MRT는 23.5°C, b 에서의 MRT는 23.2°C로 나타났다. 기존의 MRT 측정 방법과 제안된 예측 모델에서 MRT 값의 대상 공간 온도분포 차이는 1°C 미만으로 나타났다.

결 론

본 연구에서는 운영 중인 건물에서 기존 MRT 측정 방법 적용의 한계를 개선하기 위해 MRT 예측 모델을 제안하였다. 제안된 모델은 두 가지 프로세스로 진행되었다. 첫 번째 프로세스는 RC 모델 및 PSO 모델 적용을 통한 실내 표면온도 예측 모델 개발, 두 번째 프로세스는 기존의 장단파 평균복사온도 계산 알고리즘을 통한 평균복사온도 예측 모델이다. 첫 번째 프로세스에서 RC 모델 단순화를 위한 창호와 벽체의 표면온도 그룹화 방법이 제안되었다. 개발된 가상센서는 기존 IR method와 비교 검토하여 오차가 1°C 내로 발생함을 확인하였다.

제안된 가상센서는 평균복사온도 측정 방법의 실제 건물 적용을 위해 필수적으로 필요한 재실자의 활동 공간 확보, 센서 비용 최소화를 위한 대안으로 제안되었다. 이 방법은 공공 기상 데이터와 기존 센서를 활용하는 방법으로 추가적인 센서의 설치 없이 표면온도 예측이 가능하다. 본 연구에서는 대상 건물에 대한 정보를 간소화하기 위해 표면 온도를 그룹화하여 평균하였다. 따라서 그룹화 후 평균한 표면 온도는 각 표면의 실측 온도와는 차이가 발생하였다. 또한 표면 온도에 영향을 미치는 다양한 인자들 중 복사와 대류에 의한 영향만 고려하였기 때문에 표면 온도 예측 모델에서 최대 5°C가 넘는 오차가 발생한 것으로 보인다. ISO 7726 (1998)에서 Class C에 해당하는 실내 온도가 10~40°C인 공간에서 도출한 표면 온도의 정확도에 대해 ± 1°C 이내, MRT의 정확도에 대해 ± 2°C 이내를 권장하고 있다. 본 연구에서 MRT 예측 결과 오차 범위가 ± 1°C 이내로 나타난 것을 확인했다. 단기간 진행된 연구 결과는 MRT 예측 모델의 실제 건물 적용 가능성을 보여준다. 그러나 본 연구의 결과는 유사한 날씨 조건을 가진 기간 내에서 측정된 연구의 결과로 장기간 동안 발생될 수 있는 다양한 일사 조건들의 상황에서도 높은 예측성능을 확보하기 위해서는 보다 상세한 RC 모델 작성 및 장기 실험을 통한 모델 검증의 연구가 필요하다. 본 연구의 후속 연구로, 대상 건물에 대한 상세한 모델링 후 다양한 시스템 운전 상태에서의 온열 환경 평가 및 장기간 예측에 대한 연구를 수행할 예정이다.