Development of Control Algorithm for Cooling Tower Low-Approach Temperature

Ju-Wan Ha; Yu-Jin Kim; Hwan-Yong Kim; Young-Hak Song

doi:10.22696/jkiaebs.20210037

Preview

Research Article

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems. 30 October 2021. 431-442
https://doi.org/10.22696/jkiaebs.20210037

Development of Control Algorithm for Cooling Tower Low-Approach Temperature

냉각탑의 어프로치 온도 감소를 위한 제어알고리즘 개발

Ju-Wan Ha¹

Yu-Jin Kim¹

Hwan-Yong Kim²

Young-Hak Song²^*

하 주완¹

김 유진¹

김 환용²

송 영학²^*

¹Graduate Student, Graduate School, Department of Architectural Engineering, Gyeongsang National University, Jinju, Korea

²Associate Professor, Department of Architectural Engineering, ERI, Gyeongsang National University, Jinju, Korea

¹경상대학교 대학원 건축공학과 대학원과정

²경상대학교 건축공학과 부교수

^{*Corresponding Author}

ABSTRACT

The chiller efficiency is an important factor for improving the efficiency of the central chilled water system. A low-condenser water temperature is required for the low cooling tower leaving water temperature, which affects the chiller efficiency. Various studies have been conducted to produce low-condenser water temperature, but an additional review is needed on a method to lower the approach temperature. This study developed a control algorithm for cooling tower low-approach temperature. The approach temperature changes within the same load, ambient conditions according to the liquid-to-gas ratio (LGR), which is the operating condition of the cooling tower system. It found that the lower the LGR, the lower the approach temperature could be secured. As the approach temperature is lowered, it is expected that the efficiency of the chiller and cooling water pump will be improved.

Keywords

Cooling tower control

Approach temperature

Low-condenser water temperature

Cooling tower leaving water temperature

Algorithm

키워드

냉각탑 제어

어프로치온도

저온 냉각수

냉각탑 출구온도

알고리즘

MAIN

서 론
연구배경 및 목적
연구 범위 및 방법
이론적 고찰
냉각탑 모델링
수랭식 냉동기 모델링
냉각탑 제어알고리즘 개발
대상 건물 및 HVAC 시스템
어프로치온도 감소를 위한 제어 알고리즘 개발
제어알고리즘 분석결과
결 론

서 론

연구배경 및 목적

일반적으로 대형 상업용 건물에서는 중앙 냉방 시스템이 적용되며, 냉방 시스템의 다양한 구성요소 중 냉동기의 에너지 소비량은 전체 에너지 소비량의 절반 이상을 차지하고 있다(Morrison, 2015; Huang et al., 2017). 따라서 냉동기 효율 향상은 냉방시스템의 효율 개선을 위해 가장 중요한 요소이다.

냉동기의 효율을 나타내는 Coefficient of performance(이하, COP)를 향상시키기 위해서는 냉동기 출구온도, 응축기 입구온도(이하, 냉각탑 출구온도), 부분부하율, 대수제어, 주변 외기조건, 건물 부하, 시스템 구성 등 다양한 매개변수들의 영향을 고려해야 한다(Tirmizi et al., 2012; Liu et al., 2017; Wang et al., 2018; Ho and Yu, 2020). 그 중에서도 냉각탑의 냉각수 출구 온도를 낮출수록 냉각탑 팬의 에너지 사용량은 증가하는 반면, 냉동기의 냉매 압력 저하를 통한 COP 향상으로 에너지절감을 기대할 수 있다(Wang et al., 2018).

이에 저온 냉각수 생산을 위한 다양한 제어방식에 관한 연구들이 진행되고 있다. Kang et al. (2021)은 인공 신경망 기반의 중앙 냉방 시스템 실시간 예측 제어 및 최적화 알고리즘을 개발하였다. 제어 변수로 냉각탑 출구온도(25-32℃) 및 냉동기의 냉수 출구온도(6-12℃)범위를 선정하였으며, 전체 냉방시스템의 평균 에너지 절감은 7.4%, 평균 COP는 9.4% 향상되는 것으로 나타났다. 또한, 서울지역의 외기습구온도가 23℃보다 높을 경우, 어프로치온도로 +3.6 K를 제시하였다. Ha et al. (2019)은 기존 냉방시스템의 정격조건 대비 ASHRAE 90.1냉각수 설정 온도 23.9℃ 변경에 따른 냉방시스템 요소별 에너지 절감량을 정량적으로 분석하였다. 저온 냉각수 생산으로 인해 냉각탑 팬 풍량은 증가하는 반면 냉동기 에너지 감소로 연간 냉방에너지 사용량이 약 16.7%가 절감되었다. Lee et al. (2018)은 냉각수 유량제어를 통한 저온 냉각수 효과를 검증하였다. 일반적인 운전은 대부분 냉각수 온도 32℃에 분포되지만, 유량제어 알고리즘이 적용된 운전의 경우, 24℃ 정도의 낮은 온도의 냉각수를 생산할 수 있는 것으로 나타났다. 그 결과, 알고리즘 운전의 저온 냉각수 효과로 인해 냉각탑 및 VRF 실외기의 에너지 절감은 각각 24%, 5.9% 절감되었으며, 실외기 및 시스템 COP는 각각 7.3%, 12.7%가 향상되었다.

상기의 연구들에서는 저온 냉각수 생산을 위해 제어 변수로 냉각수 유량 및 설정 온도에 주안점을 두고 있으나, 냉각탑 팬 풍량을 함께 고려한 연구는 거의 없는 실정이다. 이에, 추가적으로 더 낮은 저온 냉각수 생산을 위해 냉각탑 팬 풍량에 대한 냉각수 유량 비율을 나타내는 Liquid to gas ratio(이하, LGR) 관점에서의 운전에 대한 검토가 필요하다.

일반적으로 LGR은 냉각탑 설계관점에서 검토되는 값이지만, 운전 제어 관점에서도 활용 가능하다. 동일한 사양의 시스템 내에서 LGR이 낮아지면 냉각탑 내의 공기 유량이 증가되는 것을 의미하므로 냉각수와 냉각 공기간의 접촉면적 및 냉각수의 충진재 내 잔류 시간 증가로 이어져, 충진재 특성 값을 향상시키게 된다(Kim et al., 2001). 이는 냉각탑의 냉각 능력 향상으로 이어져, 냉각탑 출구 온도와 주변 공기 습구 온도의 차이인 어프로치 온도를 낮출 수 있다. 어프로치 온도의 감소는 저온 냉각수 생산으로 이어져, 냉각탑의 입‧출구 온도차인 레인지 온도가 증가되고, 이를 통해 냉각수 유량 감소 및 냉동기 효율 향상을 기대할 수 있다. 이에, 낮은 LGR 냉각탑 운전을 통한 어프로치 온도에 대한 검토가 필요하다.

본 논문은 냉각탑부터 헤더에 이르는 수랭식 1차측 냉방시스템의 연간 에너지 효율향상을 검토하는 전체 연구의 도입부에 해당하는 것으로, LGR 관점에서의 어프로치 온도 감소 제어알고리즘 개발에 주안점을 두었다. 동일한 냉방부하 및 외기조건에서 어프로치 온도감소를 위해서는 LGR 값을 낮게 가져가야 하지만, EnergyPlus 툴에서는 냉방부하와 상관없이 유량이 일정하게 운전되는 모델링 오류가 발생하여(Unmet Hours, 2019; 2020), 변속 팬의 경우에만 LGR 값이 변화된다. 이로 인해 냉각수 유량 대비, 냉각탑 팬 풍량 감소 현상이 발생하여 어프로치온도 감소가 한계에 부딪힌다.

이를 해결하고자 이론적 고찰을 통해 어프로치 온도 산출에 필요한 변수들을 일목요연하게 재정리하고, 신규 제어 알고리즘을 개발하여 EnergyPlus에 적용 가능하도록 하였다.

연구 범위 및 방법

어프로치 온도는 냉각탑의 냉각 처리 성능을 나타내는 지표이며, 일반적으로 이 값이 작아질수록 냉각탑의 크기는 커져야 한다(Peterson, 2016). 하지만, 본 연구에서는 동일한 시스템 사양 내에서 LGR 관점에서의 운전 방식에 따른 어프로치온도 감소를 파악하고자 하였으며, 중앙 냉방시스템은 수랭식 냉동기, 변속 냉각탑 및 변유량 냉각수 펌프로 구성하였다. 또한, LGR관점에서의 제어에 필요한 냉각탑의 입구 및 출구온도, 주변공기의 습구온도, 냉각수 유량 및 냉각탑 팬 풍량 값들을 정량적으로 산출하기 위해 이론적 고찰을 실시하였다. 이를 바탕으로 어프로치 온도 감소를 위한 제어알고리즘을 개발하였으며, EnergyPlus v. 9.5에 적용하여 어프로치 온도 변화를 검토하였다.

이론적 고찰

냉각탑 모델링

냉각탑의 목적은 공기와 닿는 물의 표면적을 충진재에 극대화시켜, 증발 냉각을 최대한 활용하는 것이다(Peterson, 2016). 냉각탑 성능을 분석하기 위한 방법은 여러가지가 있으나, 본 연구에서는 EnergyPlus에 적용된 Merkel 모델을 활용하였다(DOE, 2021). 해당 모델은 냉각탑 성능을 분석하기 위해 대향류형 열교환기의 ε–NTU relationships를 이용하며, 다음과 같은 가정을 기반으로 하고 있다. (1) 공기와 수증기는 이상 기체로 작용함; (2) 물 증발 효과는 고려되지 않음; (3) 팬 가열은 고려되지 않음; (4) 접촉 경계면에서 공기는 포화상태로 가정함; (5) 루이스 수는 1로 가정함; (6) 정상상태 운전을 가정함.

냉각탑으로 들어오는 주변 공기 습구 온도와 냉각수 간의 정상상태의 총 열전달량( $d {\dot{Q}}_{t o t a l}$ )을 나타내는 방정식은 다음의 식 (1)과 같다. 또한, 공기 및 냉각수 측의 에너지 평형방정식은 식 (2) 및 (3)과 같다. 해당 식에서 습 공기의 엔탈피는 전적으로 습구온도의 함수이며, 습공기는 평균 비열( ${\bar{c}}_{p e}$ , 식 (4))을 이용하여 동등한 이상기체로써 가정하였다. 또한, 액체 측면의 전도가 기체 측면보다 훨씬 크기 때문에, 젖은 표면온도는 냉각수온도와 동일하다고 가정하였다. U_e는 식 (5)와 같으며, 이는 평균 총괄 열전달계수로, 충진재 내의 총괄 열전달계수는 동일한 것으로 가정하였다.

(1)

d {\dot{Q}}_{t o t a l} = U_{e} d A (T_{w} - T_{w b})

(2)

d {\dot{Q}}_{t o t a l} = {\dot{m}}_{w} c_{p w} (T_{i n, c w} - T_{o u t, c w})

(3)

d {\dot{Q}}_{t o t a l} = {\dot{m}}_{a} {\bar{c}}_{p e} Δ T_{w b}

(4)

{\bar{c}}_{p e} = \frac{Δ h}{Δ T_{w b}}

(5)

U_{e} = \frac{U {\bar{c}}_{p e}}{c_{p}}

여기서, U는 냉각탑 총괄열전달계수(W/m² ‧ ℃), A는 열 전달 표면적(m²), T_w는 냉각수 온도(℃), T_wb는 공기의 습구온도(℃), ${\dot{m}}_{w}$ 는 냉각수의 유량(kg/s), C_pw는 냉각수의 비열(kJ/kg ‧ ℃), ${\dot{m}}_{a}$ 는 냉각탑 팬의 풍량(kg/s), $Δ h$ 는 출구 공기의 엔탈피(h_{out, wb})와 입구 공기의 엔탈피(h_{in, wb}) 차이(J/kg), $Δ T_{w b}$ 는 출구 공기의 습구온도(T_{out, wb})와 입구 공기의 습구온도(h_{in, wb}) 차이(K), c_p는 습 공기의 비열(J/kg ‧ ℃), $T_{i n, c w}$ 는 냉각탑 입구온도(℃), $T_{o u t, c w}$ 는 냉각탑 출구온도(℃)를 나타낸다.

냉각탑의 효율은 다음의 식 (6)이 의미하는 단순 열교환기의 효율(ε_{HX, simple})과 유사하게 나타낼 수 있으며, 이 식은 냉각수의 열용량률( ${\dot{C}}_{w}$ , 식 (7))이 공기의 열용량률( ${\dot{C}}_{a}$ , 식 (8))보다 적을 때이다. 식 (1), (2)와 (3)을 합쳐 전체 열 전달 표면적에 대해 적분한 결과를 식 (6)과 결합하면 냉각탑 효율(ε_CT)에 대한 식은 다음의 식 (9)와 같이 나타난다. 여기서, NTU (Number of Transfer Units)는 식 (10)과 같으며, 이는 충진재의 특성 값으로 열전달성능을 나타내는 무차원변수이다.

(6)

ϵ_{H X, s i m p l e} = \frac{T_{i n, c w} - T_{o u t, c w}}{T_{i n, c w} - T_{i n, w b}}

(7)

{\dot{C}}_{w} = {\dot{m}}_{w} c_{p w}

(8)

{\dot{C}}_{a} = {\dot{m}}_{a} {\bar{c}}_{p e}

(9)

ϵ_{C T} = \frac{1 - \exp \{- N T U [1 - (\frac{{\dot{C}}_{w}}{{\dot{C}}_{a}})]\}}{1 - (\frac{{\dot{C}}_{w}}{{\dot{C}}_{a}}) \exp \{- N T U [1 - (\frac{{\dot{C}}_{w}}{{\dot{C}}_{a}})]\}}

(10)

N T U = \frac{U A_{e}}{{\dot{C}}_{w}}

여기서, ε_{HX, simple}는 열교환기의 효율(–), ${\dot{C}}_{w}$ 는 냉각수의 열용량률(kW/℃), ${\dot{C}}_{a}$ 는 공기의 열용량률(kW/℃), ε_CT는 냉각탑의 효율(–)을 나타낸다.

수랭식 냉동기 모델링

EnergyPlus engineering reference (DOE, 2021)에 따르면, 수랭식 냉동기의 에너지 사용량( ${\dot{P}}_{C h i l l e r}$ , 식 (11)) 은 냉방 용량 변화 곡선(f_CAP, 식 (12)), 에너지소비량 변화 곡선(f_EIR, 식 (13)), 부분 부하율 변화 곡선(f_PLR, 식 (14))에 따라 변화된다. Q_Ref 및 COP_ref는 냉동기 정격 용량 및 정격 COP를 나타내며, 해당 곡선들은 냉동기 출구 온도(T_{out, chw}), 냉각탑 출구온도(T_{out, cw}), 부분 부하율(PLR)에 따라 변화된다. 이는 냉동기 사양에 따라 상이한 값이다. 예를 들어, EnergyPlus Dataset에서 제공되는 실제 제품의 카탈로그 데이터(Carrier 19XR_1,407 kW)인 경우, 냉동기 및 냉각탑 출구 온도 범위는 각각 4.44-10℃ 및 12.78-32.22℃이며, 부분 부하율은 0.2-1.04로 명시되어 있다. 이는 시스템 효율에 영향을 미치는 요소이기 때문에, 냉동기 선정 시 검토되어야 한다.

(11)

{\dot{P}}_{C h i l l e r} = Q_{R e f} ‧ \frac{1}{C O P_{r e f}} ‧ f_{C A P} ‧ f_{E I R} ‧ f_{P L R}

(12)

f_{C A P} = α_{1} + α_{2} ‧ T_{o u t, c h w} + α_{3} ‧ T_{o u t, c h w}^{2} + α_{4} ‧ T_{o u t, c w} + α_{5} ‧ T_{o u t, c w}^{2} + α_{6} ‧ T_{o u t, c h w} ‧ T_{o u t, c w}

(13)

f_{E I R} = α_{7} + α_{8} ‧ T_{o u t, c h w} + α_{9} ‧ {T_{o u t, c h w}^{}}^{2} + α_{10} ‧ T_{o u t, c w} + α_{11} ‧ {T_{o u t, c w}^{}}^{2} + α_{12} ‧ T_{o u t, c h w} ‧ T_{o u t, c w}

(14)

f_{P L R} = α_{13} + α_{14} ‧ P L R + α_{15} ‧ P L R^{2}

여기서, T_{out, chw}는 냉동기 출구온도(℃), T_{out, cw}는 냉각탑 출구온도(℃), PLR은 부분 부하율을 나타낸다.

냉각탑 제어알고리즘 개발

대상 건물 및 HVAC 시스템

본 연구의 대상 건물은 ASHRAE 90.1 기반의 대규모 사무실 건물이며, 기준층 규모는 73.2 m(가로) × 48.8 m(세로)이며, 지상 12층, 창면적비 40%로 모델링 하였다. 대상 지역은 서울로 선정하였으며, 건물의 외피 성능은 건축물 에너지 절약설계기준에 따라 외벽 0.24 W/㎡·K, 지붕 0.15 W/㎡·K, 창 및 문 1.5 W/㎡·K, 일사 열 취득 계수(SHGC; Solar Heat gain Coefficient)는 0.516로 하였다(MOLIT, 2018).

내부 발열조건은 조명 부하 8.5 W/㎡, 기기 부하 8.07 W/㎡, 재실 밀도 18.58 ㎡/person, 최소 외기 도입량은 ASHRAE 62.1 (ASHRAE, 2019b)에 따라 9 ㎥/h·person을 적용하였다. 또한, 건물운전시간은 일반 업무용건물의 근무시간을 반영한 주 5일, 07-20 h, 냉방 설정 온도 및 Setback온도는 각각 26℃, 30℃, AHU 토출온도는 12.8℃로 고정하였다. Table 1은 대상 건물에 적용한 HVAC 시스템의 사양을 나타낸 것이다.

Table 1.

Design parameters of central chilled water system

Centrifugal chiller (2EA)	Cooling capacity	1,407 kW (400 RT)
	COP	6.04
	Chilled water flow rate	61 kg/s
	Condenser water flow rate	76 kg/s
	Chilled water temperature range	4.44-10℃
	Condenser water temperature range	12.78-32.22℃
Cooling tower (2EA)	Hear rejection	1,759 kW (400 CRT)
	Air flow rate	62 kg/s (LGR 1.2)
	Electric power(control type)	7.5 kW (Variable)
	Leaving water set temperature	14℃
Condenser water pump (2EA)	Electric power (control type/ motor efficiency)	16 kW (Variable/0.9)

어프로치온도 감소를 위한 제어 알고리즘 개발

냉각탑의 성능은 어프로치온도를 통해 나타낼 수 있으며, 냉각탑의 입구 및 출구온도, 주변공기의 습구온도, 냉각수 유량 및 냉각탑 팬 풍량에 따라 변화된다. 처음 4가지 변수는 냉방 시스템 설계자에 의해 제공되지만, 공기 유량은 냉각탑 제조사에 의해 결정된다(Peterson, 2016). 따라서 운전자가 경험 규칙(Rules of thumb)에 의존하지 않고 매시간마다 낮은 어프로치온도를 확보하기 위해서는 앞선 5가지 변수들의 관계를 고려하는 것이 중요하다.

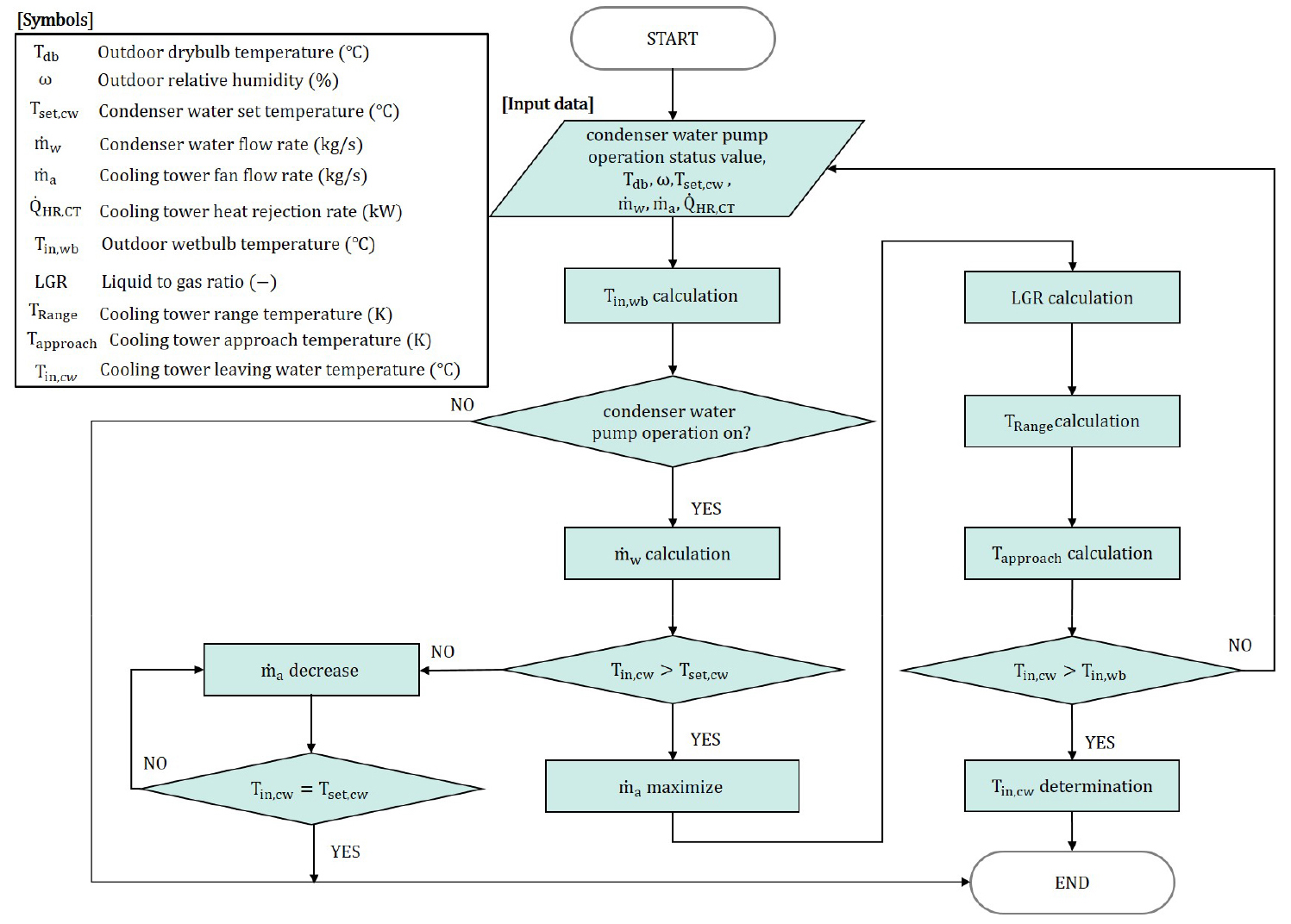
따라서 본 연구에서는 동일한 시스템 사양 내에서 동적으로 변화되는 5가지 변수들을 고려하여 낮은 어프로치 온도를 계산하는 냉각탑 제어 알고리즘을 개발하였으며, Figure 1과 같다. 해당 알고리즘은 식 (19)에서 언급하는 독립변수인 외기습구온도, LGR, 레인지 온도의 순차적 계산을 포함한다. 또한, 동일한 외기 조건 및 부하 조건인 경우, 어프로치온도는 LGR에 따라 변화하는 값이므로 제어단계마다 낮은 LGR을 유지하는 것에 주안점을 두었다. LGR을 낮출수록 냉각탑의 효율 향상을 통해, 어프로치온도를 감소시킬 수 있으며, 이를 통해 냉각수 유량 감소 및 냉동기 COP 향상을 기대할 수 있다.

https://static.apub.kr/journalsite/sites/kiaebs/2021-015-05/N0280150502/images/Figure_KIAEBS_15_5_02_F1.jpg

Figure 1.

cooling tower control algorithm for Low-approach temperature

알고리즘 제어에 필요한 입력데이터는 외기 건구온도 및 상대습도, 냉각수 설정 온도, 냉각수 유량, 냉각탑 팬 풍량, 냉각탑 처리 열량, 냉각수 펌프 가동 여부이다. 해당 입력데이터를 활용하여 어프로치 온도 계산에 필요한 제어 변수들을 재 산출하였다.

먼저, 냉각수 설정 온도는 기존 연구들(Lee et al., 2018; Ha et al., 2019; Kang et al., 2021)에서 ASHRAE 90.1 (ASHRAE, 2019a) 기준의 약 24℃로 설정되고 있다. 하지만, 서울 지역(기후 존 4A)인 경우, 평균 외기 습구온도는 냉방기 및 중간기 각각 11.2-18.2℃, 2.3-12.6℃로 나타났다(Ha et al., 2020). 이에 추가적인 냉방 시스템 효율 개선 및 에너지절감을 위해서 냉각수 설정온도를 냉동기의 하한온도까지 낮출 수 있다. 따라서 본 연구의 냉각수 설정 온도는 냉동기(Carrier 19XR_1,407 kW)모델의 사양을 참조하여, 14℃로 설정하였다. 이는 해당 모델의 하한 온도 값인 12.78℃에 여유율 약 10%를 추가한 값이며, 냉방사이클의 안정적인 유지를 위해 보수적으로 설정한 값이다.

다음으로 외기습구온도의 경우 습구온도계를 이용하여 측정이 가능하지만, 대부분의 건물에서는 해당 데이터 취득이 어렵다. 이에 일반적으로 건물에서 측정하는 건구온도(T_db) 및 상대습도(ω)의 값을 다음의 식 (15)에 대입하여 습구온도(T_{in, wb})를 계산하였다(Stull, 2011).

(15)

T_{i n, w b} = T_{d b} ‧ atan [0.151977 (ω + 8.313659)^{0.5}] + atan (T_{d b} + ω) - atan (ω - 1.676331) + 0.00391838 (ω)^{1.5} ‧ atan (0.023101 ω) - 4.686035 .

여기서, T_db는 건구온도(℃), ω는 상대습도(%), T_{in, wb}는 습구온도(℃)를 나타낸다.

냉방시스템의 가동 상태는 냉각수펌프의 on/off를 통해 판단하며, 냉각수 유량( ${\dot{m}}_{w}$ )은 다음의 식 (16)을 통해, 재 산출하였다. 앞서 언급하였듯이 현재 EnergyPlus 시뮬레이션 프로그램에서는 건물의 냉방 부하 및 변속 냉각수 펌프의 작동과 관계없이 냉동기가 운전될 때마다 연중 내내 냉각수 펌프 유량이 일정하게 유지되며, 냉각탑 팬의 변속제어만 구현되는 문제점이 있다(Unmet Hours, 2019; 2020). 이를 해결하기 위해 냉각탑의 처리 열량( ${\dot{Q}}_{H R, C T}$ ) 비율에 따라 냉각수 유량을 실시간으로 조절하였다.

(16)

{\dot{m}}_{w} = {\dot{m}}_{R e f, w} ‧ \frac{{\dot{Q}}_{H R, C T}}{{\dot{Q}}_{R e f, C T}}

여기서, ${\dot{m}}_{w}$ 는 냉각수 유량(kg/s), ${\dot{m}}_{R e f, w}$ 는 정격 조건의 냉각수 유량(kg/s), ${\dot{Q}}_{H R, C T}$ 는 냉각탑의 처리 열량(kcal/h), ${\dot{Q}}_{R e f, C T}$ 는 정격조건의 냉각탑 처리 열량(kcal/h)을 나타낸다.

EnergyPlus engineering reference (DOE, 2021)에 따르면 어프로치 온도 감소를 위해 본 연구에 적용된 변속 냉각탑 모델인 경우 우선적으로 냉각탑 팬을 최대 속도로 운전 시켜 냉각탑 출구온도를 결정하고, 냉각탑 출구온도가 설정 온도에 비해 높은 경우, 냉각탑 팬이 계속하여 최대 속도로 유지된다. LGR은 식 (17)을 이용하여 산출하였다.

(17)

LGR = \frac{{\dot{m}}_{w}}{{\dot{m}}_{a}}

레인지 온도(T_Range)는 다음의 식 (18)으로 계산하였으며, 여기서 C_pw는 물의 비열 값인 4.185 kJ/kg‧℃에 해당된다. T_Range는 앞선 식 (16)에서 계산된 유량이 줄어들수록 커지게 되므로, 이는 냉방 부하에 따라 변화하는 값으로 해석할 수 있다.

(18)

T_{R a n g e} = \frac{{\dot{Q}}_{H R, C T}}{{\dot{m}}_{w} ‧ C_{p w}}

본 연구에 적용된 변속 냉각탑의 YorkCalc 모델 어프로치온도는 다음의 식 (19)를 통해 산출할 수 있다. 여기서, $β_{1} - β_{27}$ 은 냉각탑모델의 특성을 나타내는 계수이며, Table 2와 같다(DOE, 2021). 해당 식의 종속변수인 어프로치온도는 식 (15), (17), (18)에서 계산된 외기 습구온도, 레인지온도 및 LGR을 대입하여 산출할 수 있으며, 해당 독립 변수들 값에 따라 변화되는 값이다.

(19)

T_{a p p r o a c h} = β_{1} + β_{2} ‧ T_{i n, w b} + β_{3} ‧ {T_{i n, w b}^{}}^{2} + β_{4} ‧ T_{R a n g e} + β_{5} ‧ T_{i n, w b} ‧ T_{R a n g e} + β_{6} ‧ {T_{i n, w b}^{}}^{2} ‧ T_{R a n g e} + β_{7} ‧ {T_{R a n g e}^{}}^{2} + β_{8} ‧ T_{i n, w b} ‧ {T_{R a n g e}^{}}^{2} + β_{9} ‧ {T_{i n, w b}^{}}^{2} ‧ {T_{R a n g e}^{}}^{2} + β_{10} ‧ L G R + β_{11} ‧ T_{i n, w b} ‧ L G R + β_{12} ‧ {T_{i n, w b}^{}}^{2} ‧ L G R + β_{13} ‧ T_{R a n g e} ‧ L G R + β_{14} ‧ T_{i n, w b} ‧ T_{R a n g e} ‧ L G R + β_{15} ‧ {T_{i n, w b}^{}}^{2} ‧ T_{R a n g e} ‧ L G R + β_{16} ‧ T {_{R a n g e}^{}}^{2} ‧ L G R + β_{17} ‧ T_{i n, w b} ‧ {T_{R a n g e}^{}}^{2} ‧ L G R ‧ {T_{i n, w b}^{}}^{2} ‧ {T_{R a n g e}^{}}^{2} ‧ L G R + β_{19} ‧ L G R^{2} + β_{20} ‧ T_{i n, w b} ‧ L G R^{2} + β_{21} ‧ T_{i n, w b} ‧ L G R^{2} + β_{22} ‧ T_{R a n g e} ‧ L G R^{2} + β_{23} ‧ T_{i n, w b} ‧ T_{R a n g e} ‧ L G R^{2} + β_{24} ‧ {T_{i n, w b}^{}}^{2} ‧ T_{R a n g e} ‧ L G R^{2} + β_{25} ‧ {T_{Range}^{}}^{2} ‧ L G R^{2} + β_{26} ‧ T_{i n, w b} ‧ {T_{R a n g e}^{}}^{2} ‧ L G R^{2} + β_{27} ‧ {T_{i n, w b}^{}}^{2} ‧ {T_{R a n g e}^{}}^{2} ‧ L G R^{2}

Table 2.

Cooling tower model coefficients

β₁	β₂	β₃	β₄	β₅
-0.359741205	-0.055053608	0.0023850432	0.173926877	-0.0248473764
β₆	β₇	β₈	β₉	β₁₀
0.00048430224	-0.005589849456	0.0005770079712	-1.342427256E-05	2.84765801111111
β₁₁	β₁₂	β₁₃	β₁₄	β₁₅
-0.121765149	0.0014599242	1.680428651	-0.0166920786	-0.0007190532
β₁₆	β₁₇	β₁₈	β₁₉	β₂₀
-0.025485194448	4.87491696E-05	2.719234152E-05	-0.06537662555556	-0.002278167
β₂₁	β₂₂	β₂₃	β₂₄	β₂₅
0.0002500254	-0.0910565458	0.00318176316	3.8621772E-05	-0.0034285382352
β₂₆	β₂₇
8.56589904E-06	-1.516821552E-06

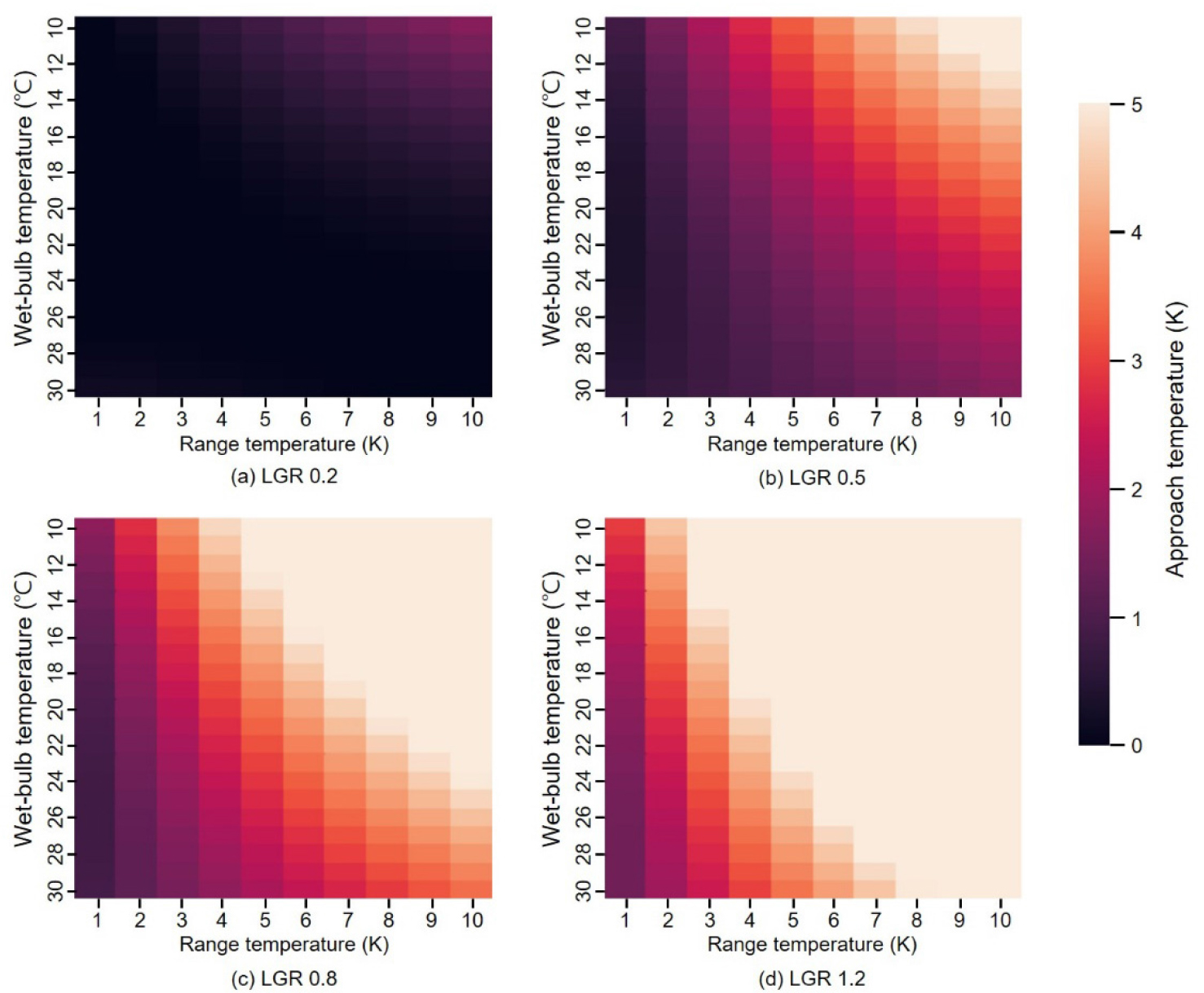
이에 동일한 외기 습구온도 및 부하조건에서 낮은 어프로치 온도를 확보하기 위해서는 LGR을 줄여야 한다. LGR을 줄이기 위해서는 냉각수 유량을 줄이거나 냉각탑 팬 풍량을 증가시켜야 한다. 하지만, 앞서 설명하였듯이 냉각수 유량은 부하의 영향을 받으므로 건물의 운영자가 임의로 변경하는데 한계가 있다. 따라서, 냉각탑 설정 온도보다 냉각탑 출구온도가 높은 경우, 운전자는 냉각탑 팬 최대 속도 운전이 우선적으로 고려되어야 동일 조건에서 낮은 LGR달성이 가능하다. LGR에 따른 어프로치 온도변화는 정량적으로 검토 가능하며, 다음의 Figure 2와 같다.

https://static.apub.kr/journalsite/sites/kiaebs/2021-015-05/N0280150502/images/Figure_KIAEBS_15_5_02_F2.jpg

Figure 2.

Approach temperature according to variable LGR

냉각수 유량 증가 및 냉각탑 팬 풍량이 감소되면 LGR이 높아져 어프로치 온도가 오히려 증가되기 때문에 제외하여 나타냈으며, LGR 1.2 값은 냉각탑시스템의 정격 운전시의 값이다. LGR이 낮은 상태에서 운전할수록 동일한 조건내에서도 더 낮은 어프로치온도가 확보 가능하다. 이에 냉각탑 시스템 운전시 시스템 사양 내에서, 가능한 LGR을 낮추는 것이 냉동기 효율 향상에 기여한다고 사료된다.

식 (20)의 냉각탑 출구온도(T_in,cw)는 식 (15)의 습구온도 및 (19)의 어프로치온도를 이용하여 재 산출한 것이다. 여기서 계산된 값은 냉각탑 설정 온도 및 외기 습구온도 보다 높은 값이다.

(20)

T_{i n, c w} = T_{i n, w b} + T_{a p p r o a c h}

여기서, T_in,cw는 냉각탑 출구온도(℃)를 나타낸다.

제어알고리즘 분석결과

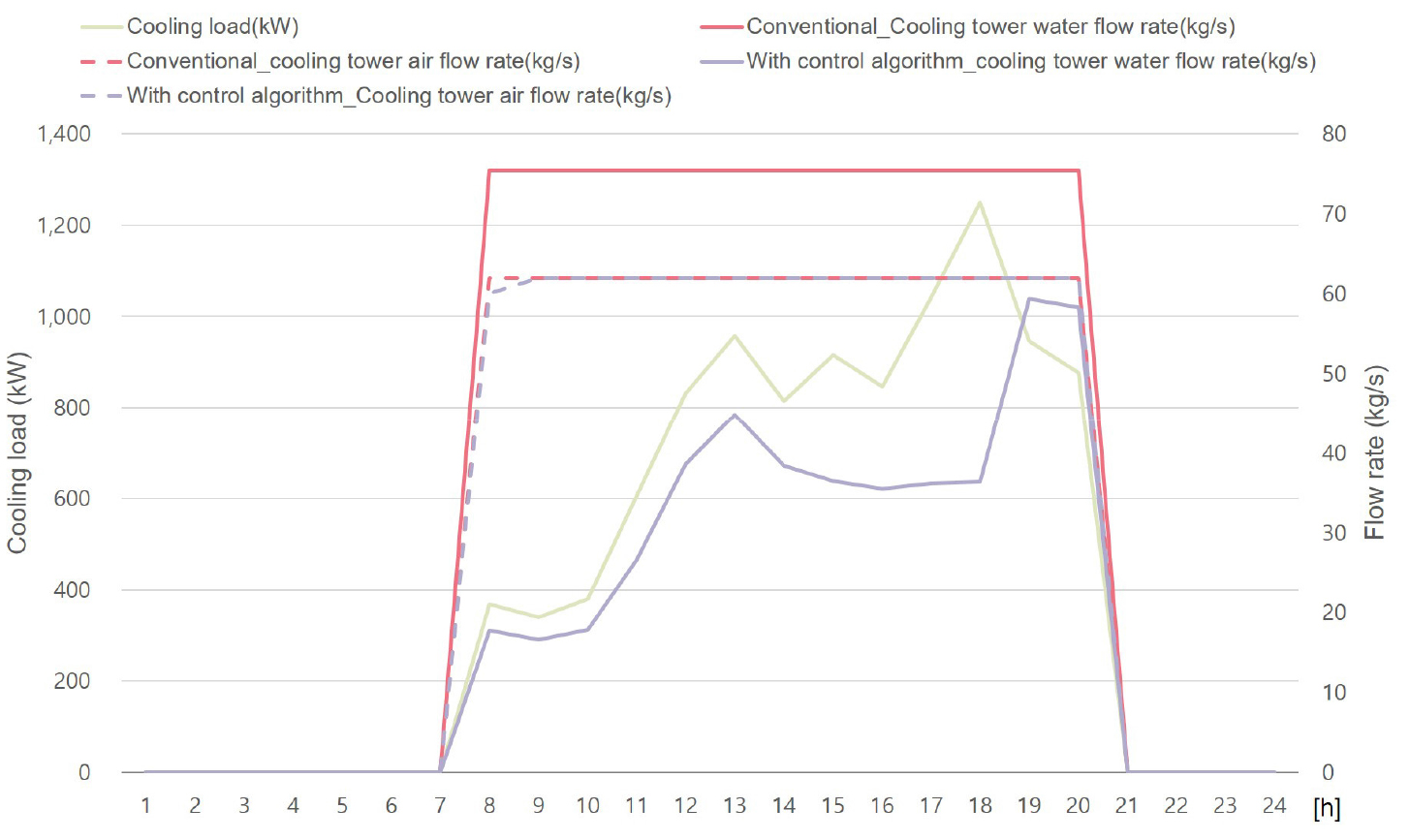
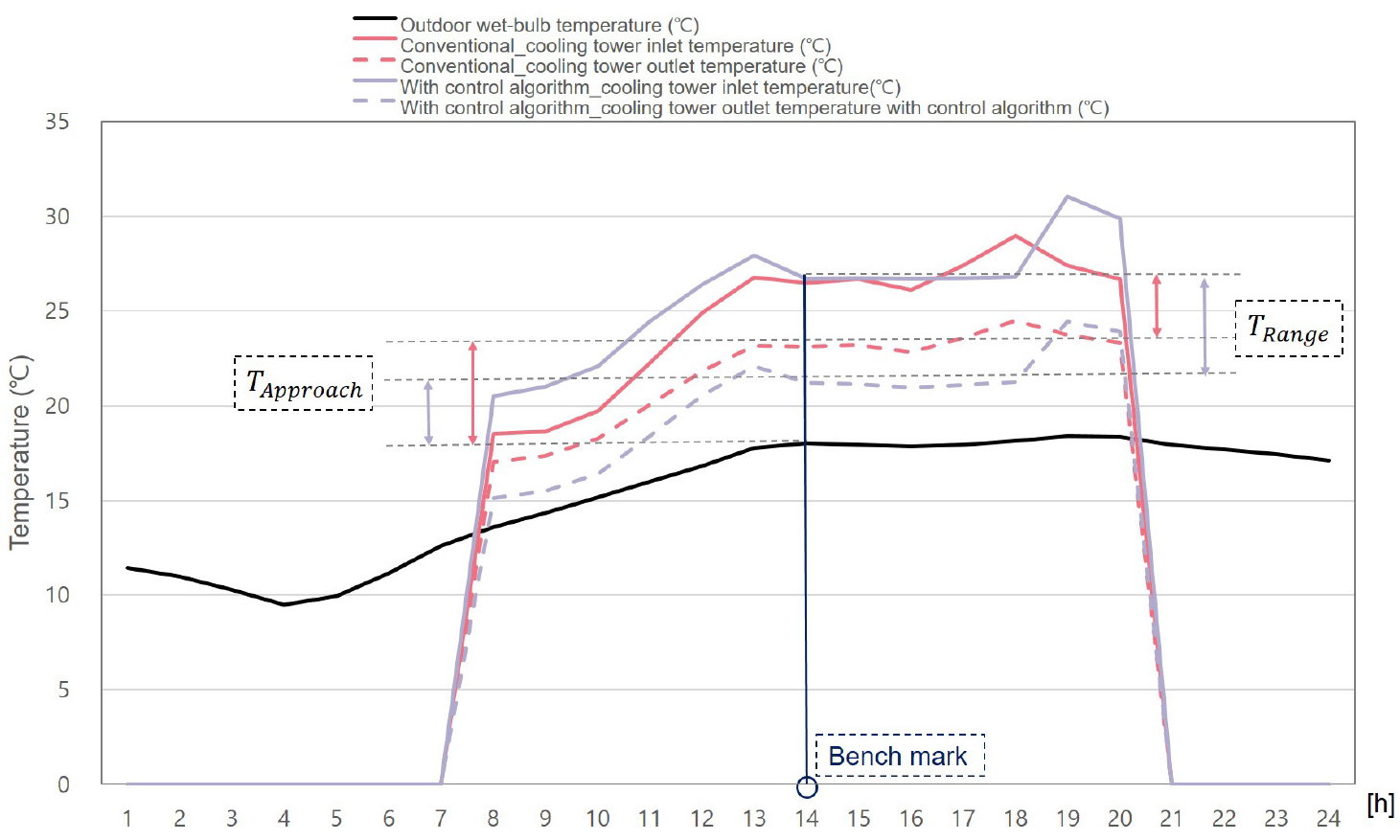
다음의 Figure 3은 동일한 부하일 때의 제어 알고리즘 적용 유무에 따른 냉각수 유량 및 냉각탑 팬 풍량을 나타낸 것이며, Figure 4는 외기습구온도에 따른 냉각탑 입 출구온도를 나타낸 것이다. 해당 그림에서 일반적인 운전 방식은 냉각수 펌프 유량이 일정한 상태이며, 알고리즘이 적용된 경우는 부하에 따라 유량이 조절되며, 운전 범위 내에서 낮은 LGR을 유지하기 위하여, 냉각탑 팬 풍량이 최대로 운전되는 방식이다. 제어알고리즘은 동적 시뮬레이션 프로그램인 EnergyPlus v. 9.5에 Python EMS Script를 적용하였다. 어프로치 온도는 냉방기 및 중간기 동안 파악할 수 있으나, 냉방기에 비해 중간기의 어프로치온도 감소효과가 극명하므로 시뮬레이션 결과는 중간기(4-5, 10,11월)의 평균부하조건인 5월 10일로 선정하여 나타냈다.

https://static.apub.kr/journalsite/sites/kiaebs/2021-015-05/N0280150502/images/Figure_KIAEBS_15_5_02_F3.jpg

Figure 3.

Cooling tower air and water flow rate according to control algorithm application (May. 10)

https://static.apub.kr/journalsite/sites/kiaebs/2021-015-05/N0280150502/images/Figure_KIAEBS_15_5_02_F4.jpg

Figure 4.

Range and approach temperature according to control algorithm application (May. 10)

동일한 부하 조건 내에서 냉각탑 제어 알고리즘이 적용된 경우는 냉각탑 팬 풍량 및 유량 변경이 가능하다. 낮은 LGR으로 냉각탑을 운전하기 위해, 냉각탑 팬 운전을 최대 풍량으로 유지하였으며, 부하 변동에 따라 냉각수 유량이 조절되고 있는 것으로 나타났다. 이에 냉각수 유량이 감소되면 레인지온도가 증가하게 되며, 이로 인해 어프로치온도를 더 낮출 수 있다. 14시 기준으로 알고리즘 적용 전인 일반적인 제어 방식은 레인지 온도 3.5 K, 어프로치 온도 5.2 K, 알고리즘이 적용 후는 레인지 온도 5.6 K, 어프로치 온도 3.2 K로 나타났다. 알고리즘이 적용되었을 때 레인지 온도는 2.1 K 증가되었으며, 어프로치온도는 2 K 감소된 것으로 나타났다. 이에 냉각수 유량 감소 및 어프로치온도 감소로 인한 냉각수 펌프 동력 감소 및 냉동기 효율 향상을 기대할 수 있을 것으로 사료된다.

결 론

본 논문은 어프로치 온도를 감소시켜 냉각수 온도 저감에 따른 중앙 냉방시스템 효율향상 및 에너지 절감에 대한 연구의 일환으로서 이론적 고찰을 통해 어프로치 온도 감소를 위한 냉각탑 제어 알고리즘을 개발하였다. 선행 연구(Lee et al., 2018)에서는 냉각수 유량 감소를 통해 낮은 냉각수 온도를 생산하였으나, 추가적으로 낮은 저온 냉각수를 생산하기 위해서는 냉각탑 팬 풍량을 함께 고려한 LGR관점에서의 제어가 필요한 것으로 판단된다.

동일한 외기 조건 및 부하 조건내에서도, LGR에 따라 어프로치 온도가 변화되며, LGR을 낮출수록 낮은 어프로치온도를 확보 가능한 것으로 나타났다. 낮은 LGR은 냉각탑 시스템 사양 내에서 냉각수 유량 감소 및 냉각탑 팬 풍량 증가로 달성할 수 있다. 설정 온도보다 냉각수 온도가 높을 경우, 냉각수 펌프 유량은 부하에 따라 변화되는 값이므로 낮은 어프로치 온도 달성을 위해서는 냉각탑 팬 풍량 증가가 우선되어야 된다고 사료된다. 또한, 해당 알고리즘을 통해 추가적인 고효율 장치 없이 냉각탑 제어 알고리즘 변경만으로도 시스템 효율 향상에 기여할 수 있을 것으로 기대된다.

동일한 부하조건에서 어프로치 온도를 낮출수록, 레인지 온도가 커지게 되어 냉각수 유량이 줄어들게 된다. 본 연구에서 개발된 알고리즘은 기존에 개발된 알고리즘 대비 냉각탑 팬 풍량이 증가되므로 낮은 어프로치 온도로 인한 냉동기 및 냉각수펌프의 에너지 절감에 대한 검토가 필요할 것으로 판단된다. 이에, 향후의 연구에서는 본 논문에서 개발된 냉각탑 제어알고리즘을 활용하여 최종적으로 매시간 마다 변화되는 건물부하 및 외기 조건을 반영한 동적 시뮬레이션을 통해 중앙 냉방시스템 효율향상 및 에너지절감에 대한 자세한 검토는 향후의 연구 성과물에서 다룰 예정이다.

Acknowledgements

이 성과는 2021년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2017R1A2B2006424).

References

Ha, J.W., Cho, S.Y., Kim, H.Y., Song, Y.H. (2020). Annual Energy Consumption Cut-Off with Cooling System Design Parameter Changes in Large. Energies, 13(8), 2034. 10.3390/en13082034

Ha, J.W., Park, K.S., Kim, H.Y., Song, Y.H. (2019). A study on Annual Cooling Energy Consumption Cut-off with Cooling Tower Control Change. Journal of KIABES, 13(6), 503-514. 10.3390/en13082034

Ho, W.T., Yu, F.W. (2020). Improved model and optimization for the energy performance of chiller system with diverse component staging. Energy, 217, 119376. 10.1016/j.energy.2020.119376

Huang, S., Zuo, W., Sohn, M.D. (2017). Improved cooling tower control of legacy chiller plants by optimizing the condenser water set point. Building and Environment, 111, 33-46. 10.1016/j.buildenv.2016.10.011

Kang, W.H., Yoon, Y., Lee, J.H., Song, K.W., Chae, Y.T., Lee, K.H. (2021). In-situ application of an ANN algorithm for optimized chilled and condenser water temperatures set-point during cooling operation. Energy and Buildings, 233, 110666. 10.1016/j.enbuild.2020.110666

Kim, J.H., Choi, C.H., Kang, B.H., Lee, J.H. (2001). Effects of Hydrophilic Treatment by IAR Method on the Packing Characteristic Value. Transactions of the Korean Society of Mechanical Engineers, B25(4), 554-560.

Lee, J.H., Kim, H.M., Song, Y.H. (2018). A Study on verification of changes in performance of a water-cooled VRF system with control change based on measuring data. Energy and Buildings, 158, 712-720. 10.1016/j.enbuild.2017.10.014

Liu, Z., Tan, H., Luo, D., Yu, G., Li, J., Li, Z. (2017). Optimal chiller sequencing control in an office building considering the variation of chiller maximum cooling capacity. Energy and Buildings, 140, 430-442. 10.1016/j.enbuild.2017.01.082

Morrison, F. (2015). Saving water with cooling towers. ASHRAE Journal, 57, 20-33.

Peterson, K.W. (2016). Open cooling tower design considerations. ASHRAE Journal, 58, 50-54.

Stull, R. (2011). Wet-bulb temperature from relative humidity and air temperature. Journal of Applied meteorology and climatology, 50, 2267-2269. 10.1175/JAMC-D-11-0143.1

Tirmizi, S.A., Gandhidasan, P., Zubair, S.M. (2012). Performance analysis of a chilled water system with various pumping schemes. Applied Energy, 100, 238-248. 10.1016/j.apenergy.2012.05.052

Wang, L., Lee, E.W.M., Yuen, R.K.K. (2018). A practical approach to chiller plants' optimisation. Energy and Buildings, 169, 332-343. 10.1016/j.enbuild.2018.03.076

American Society of Heating, Refrigerating and Air-conditioning Engineers (ASHRAE). (2019a). Energy Standard for Buildings Except Low-Rise Residential Buildings; ASHRAE Standard 90.1; ASHRAE: Atlanta, GA, USA.

American Society of Heating, Refrigerating and Air-conditioning Engineers (ASHRAE). (2019b). Ventilation for Acceptable Indoor Air Quality; ASHRAE Standard 62.1; ASHRAE: Atlanta, GA, USA.

Department of Energy (DOE). (2021). Energyplus Engineering Reference.

Ministry of Land, Infrastructure and Transport (MOLIT). (2018). Building Energy Saving Design Standards; Sejong, Korea.

Unmet Hours: Question-and-Answer Resource for the Building Energy Modelling Community. (2019). Available at: https://unmethours.com/question/35540/condenser-loop-pumpvari ablespeed-always-running/.

Unmet Hours: Question-and-Answer Resource for the Building Energy Modelling Community. (2020). Available at: https://unmethours.com/question/54977/how-to-simulate-a-variable- speed-condenser-water-pump-in-energyplus/.

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems ISSN:1976-6483(Print) 2586-0666(Online) 한국건축친환경설비학회논문집

Preview

Development of Control Algorithm for Cooling Tower Low-Approach Temperature

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

Table 1.

Design parameters of central chilled water system

Figure 1.

cooling tower control algorithm for Low-approach temperature

(15)

(16)

(17)

(18)

(19)

Table 2.

Cooling tower model coefficients

Figure 2.

Approach temperature according to variable LGR

(20)

Figure 3.

Cooling tower air and water flow rate according to control algorithm application (May. 10)

Figure 4.

Range and approach temperature according to control algorithm application (May. 10)

Acknowledgements

References