서 론
실험개요
실험체의 구성
측정방법
실험Case
실험결과
환기캡 형상별 유량 및 레이놀즈수와 정압 손실의 관계
유량 및 레이놀즈수에 의한 정압 손실의 회귀식
환기캡 형상과 정압 손실 및 손실계수 KL의 상관관계 분석
CFD의 물리적 재현성 및 신뢰도 확인
CFD 해석 개요
CFD 해석 결과
CFD를 이용한 환기캡 직경에 따른 정압 손실 해석
CFD 해석 개요
CFD해석 결과
결 론
서 론
단독 및 공동주택에서 사용되는 환기설비(주방 후드, 욕실 환기팬, 전열교환기 등)는 중앙 집중식 건축물의 환기설비보다 정압이 낮고 환기량이 매우 작다. 낮은 정압으로 인해 덕트의 계통과 입구 및 출구 영역의 형상적 특징에 의해 발생하는 정압 손실이 환기설비에 의한 환기량에 매우 큰 영향을 미친다. 주택의 환기설비 계통에는 알루미늄 플렉시블 덕트가 많이 사용되고 있고, 플렉시블 덕트에서의 정압 손실 및 환기량에 관한 연구로 손유라와 양정훈 (2020), 조성민 (2007) 등이 있다.
입구 및 출구 영역의 말단에는 “환기캡” 또는 “후드캡”이 설치되는데(이후 환기캡으로 칭함), 이곳을 통해 직접적으로 신선 외기의 도입 또는 실내 오염공기의 배출이 이루어진다. 환기캡은 형상과 연결 덕트의 직경이 다양하고, 그에 따라 정압 손실과 손실계수가 변화할 수 있다. 효율적인 환기시스템 설계를 위해서 환기캡 형상과 직경에 대한 정압 손실과 손실계수에 대한 정보가 필요하다. 또한 환기캡의 형상 중 어떤 특성이 정압 손실과 손실계수에 많은 관계가 있는지를 분석하여 이후 환기캡의 개발에 정보를 줄 수 있다.
김옥 외 (2006)는 고층 공동주택을 가정하여 4종류의 환기캡에 대한 배기성능을 평가하였다. 이때 외부 풍속 및 풍향의 변화를 중요한 변수로 활용하였다. Kang et al. (2017)은 아파트에 설치되는 주방 후드의 배기성능을 향상에 기여할 수 있는 요소를 조사하였다. 그 요소 중 하나로 환기캡이 선정되었고, 개방 면적이 중요함을 강조하였다. Lin et al. (2018)은 주택에서 사용하는 주방 후드의 환기 성능을 높이기 위하여 외기 도입용 환기캡의 설치위치 및 개수에 대하여 연구하였다. 이상의 연구들에서는 환기캡의 중요성과 기능에 대하여는 상세히 검토되었으나, 환기캡의 종류 및 직경에 따른 정압 손실 및 손실계수에 대한 자세한 정보는 찾을 수 없었다.
본 연구의 목적은 직배기 환기설비의 출구 영역에 설치되는 환기캡의 형상 및 직경이 정압 손실 및 손실계수와 기류 특성에 어떤 영향을 미치는지 분석하는 데에 있다. 특히, 본 연구에서는 배기를 중심으로 한 직배기용 환기캡에 주목하고, 실험과 CFD (Computational Fluid Dynamics)를 수행하였다. 실험은 주방 후드와 욕실 환기팬의 직배기 계통에서 주로 사용되는 직경 100 mm인 8개 종류의 환기캡을 대상으로 정압 손실 및 손실계수를 산출하고, P-Q 곡선과 P-Re 곡선을 제시하였다. 상관분석을 이용해 환기캡 형상 중 어떤 변수가 정압 손실과 손실계수에 더 많은 상관이 있는지를 분석하였다. 실험을 CFD로 재현하여 해석 모델의 신뢰성을 검토하였다. 실험에서 재현하지 못한 직경 변화에 따른 기류 특성을 비교하기 위해서 일반적으로 많이 사용되는 2종류의 환기캡을 대상으로 CFD를 이용하여 정압 손실을 검토하고, 기류 특성을 분석하였다.
실험개요
실험체의 구성
Figure 1은 본 연구의 실험체 구성을 나타내었다. 실험체는 고풍량 송풍기(2280 m3/h), 이형 소켓(Reducer), 100 mm PVC관 및 풍량 조절 댐퍼, 평균 피토관 Debimo Blade(이후 Debimo)를 연결해 구성하였다. 실제 환기캡이 설치되는 경우 환기캡과 연결되는 관은 플렉시블 덕트이다. 하지만 본 연구는 환기캡의 정압 손실을 측정하기 위해 플렉시블 덕트의 설치 없이 Figure 1과 같이 구성하였다. 이형 소켓은 직경감소에 의한 압력손실을 감소시키기 위해 250 mm × 200 mm, 200 mm × 150 mm, 150 mm × 100mm 세 개의 이형 소켓을 연결하여 사용하였다. 실험체에서 공기는 고풍량 송풍기에서 환기캡의 방향으로 배출되었다. Debimo의 제조사는 안전거리를 풍상측에 10D, 풍하측에 5D로 제안하였다(KIMO Debimo Blade Manual). 안전거리를 만족시키기 위해 풍상측과 풍하측에 10D의 PVC관을 설치하였다. 실험 대상인 환기캡은 국내에서 사용되는 환기캡 8가지를 선정하였고, 실험체 말단에 설치하였다.
측정방법
Table 1은 실험에 사용한 측정장비의 개요이다. Debimo는 피토관의 원리를 이용하여 전압과 정압을 측정한다(손유라 외, 2019). Debimo로 측정된 전압과 정압의 압력차를 KIMO사의 차압계 MP210을 이용하여 동압을 얻었다. 측정된 동압은 식 (1)을 이용하여 유량을 산출하였다. 대기압은 Testo 511을 이용하여 측정하였다. 실험체 계통의 온도 측정은 T-type 열전대를 이용하였다. 환기캡 직전 100 mm PVC관 1D에 상, 하, 우측(S1, S2, S3)에 직경 10 mm인 KIMO사의 Ref.483 압력 커넥터를 설치하여 압력을 측정하였다.
Table 1.
Measurement equipment overview
여기서, v는 유속[m/s], CF는 Debimo blade의 계수 0.8165, △P는 Debimo에서 측정된 전압과 정압의 압력차[Pa], ρ는 밀도[kg/m3]을 의미한다(KIMO). 이때 사용되는 밀도는 Debimo의 매뉴얼에 따라 식 (3)을 이용하여 산출하였다(KIMO). 직선 관로인 PVC관에서 여러 형상과 개방 면적을 가지고 있는 환기캡으로 공기가 배출되면서 정압 손실이 발생한다. 모든 수두 손실 정보는 무차원 형태로 주어지며 손실계수로 표현된다(White, 2011). 환기캡은 직관이 아닌 추가적인 부품으로 관 시스템의 전반적인 수두 손실을 증가시키며 이러한 손실을 부차적 손실이라 한다. 부차적 손실계수는 식 (3)을 이용하여 산출하였다. 여기서 KL은 손실계수, △P는 S1, S2, S3에서 측정된 정압 차의 평균값이다.
실험Case
Table 2는 실험 Case를 나타낸다. 실험은 국내 환기캡 중 실제로 사용되고 있는 직경이 100 mm인 8가지 환기캡을 대상으로 하였다. 풍량 조절 댐퍼를 완전히 개방하여 최대 풍속으로 실험을 하였고, 최대풍속에서부터 2 m/s씩 풍속을 감소시키며 실험하였다.
실험결과
환기캡 형상별 유량 및 레이놀즈수와 정압 손실의 관계
환기캡의 형상에 따라 실험으로 재현할 수 있는 최대 풍속이 달랐다. 환기캡 No. 2의 최대풍속은 10.5 m/s로 가장 큰 풍속을 재현할 수 있었다. 환기캡 No. 4와 환기캡 No. 8은 최대 풍속이 5.8 m/s와 4.4 m/s로 두 개의 풍속 Case를, 환기캡 No. 7은 최대 풍속 2.4 m/s로 하나의 풍속 Case를 재현할 수 있었다.
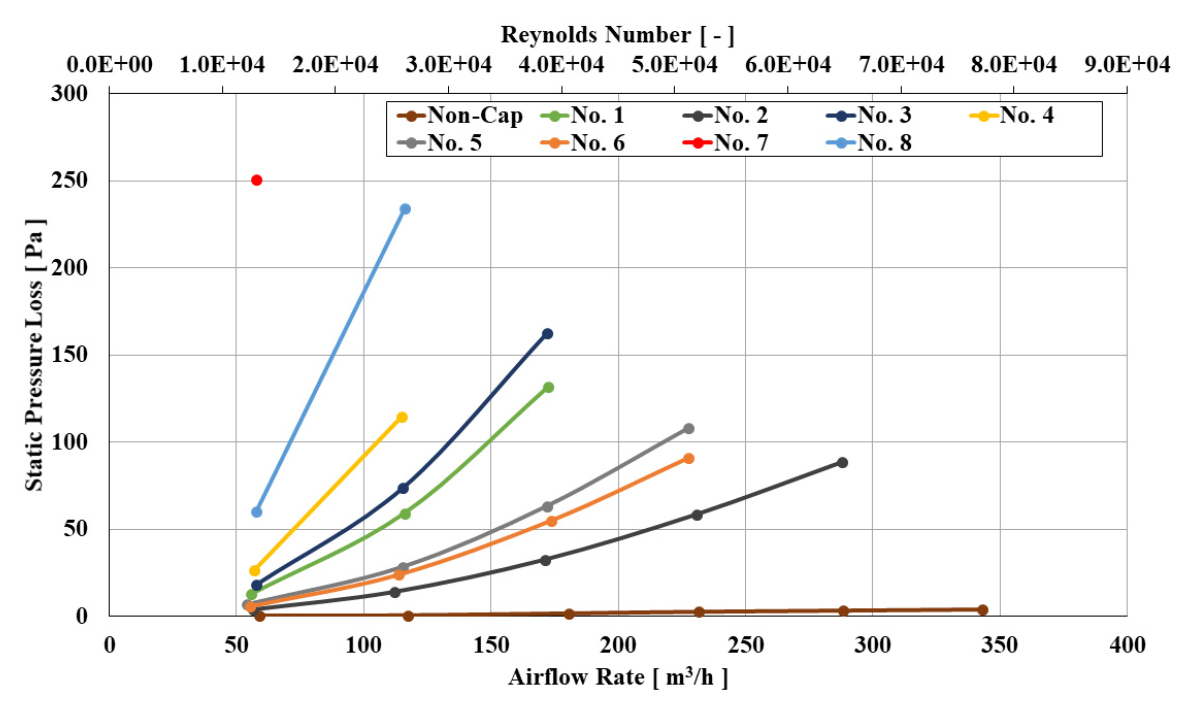
Figure 2는 실험 Case에서 측정된 유량 및 레이놀즈수와 정압 손실의 관계를 나타내었다. 레이놀즈수는 밀도, 풍속, 직경, 점성계수로 산출했다. 이때 밀도와 풍속은 식 (2)와 식 (3)을 이용했다. 유량과 정압 손실의 관계를 나타내는 그래프와 레이놀즈수와 정압 손실의 관계를 나타내는 그래프는 같은 양상을 보였다. “Non-Cap”은 환기캡을 설치하지 않은 실험체에서 측정된 실험 결과이다. 풍속이 2 m/s일 때, 환기캡 No. 7에서 250.97 Pa로 가장 큰 정압 손실이 발생하였으며, 환기캡 No. 2에서 3.77 Pa로 가장 작은 정압 손실이 발생하였다.
유량 및 레이놀즈수에 의한 정압 손실의 회귀식
환기캡은 환기 시스템에서 값이 저렴하고 가장 말단에 설치되어 시공자와 사용자가 큰 고려를 하지 않는다. 하지만 환기캡에서도 많은 정압 손실이 발생되었다. 정확한 배출 유량과 유입 유량을 예측하면 과도한 설계를 하지 않아도 되며 환기장치의 기능을 최대한 발휘할 수 있다. 환기장치에서 중요한 지표로 활용되는 P-Q곡선과 P-Re곡선을 이용하여 환기장치를 설계할 때 배출 유량과 유입 유량을 예측할 수 있다(최선호와 이건태, 2012).
Table 3는 환기캡 형상별 유량 및 레이놀즈수에 따른 정압 손실 회귀방정식을 나타낸다. 유량과 정압 손실에 대한 회귀식은 AR (Airflow Rate)로 레이놀즈수와 정압 손실에 대한 회귀식은 Re (Reynolds number)로 표기하였다. 실험 Case마다 재현된 풍속이 다르기 때문에 다른 유효범위를 가지고 있다. 환기캡 No. 4, No. 7, No. 8은 3가지 이상의 풍속 Case 실험이 불가능하여 회귀식을 도출할 수 없었다. 환기캡 No. 2의 유량과 정압 손실에 대한 회귀식은 거듭제곱 형식이며, 그 외 환기캡은 유량과 정압 손실에 대한 회귀식과 레이놀즈수와 정압손실에 대한 회귀식 모두 이차방정식 형식으로 나타났다.
Table 3.
Static pressure loss regression equation according to airflow rate and reynolds number by ventilation cap models (y : static pressure loss (Pa), x : airflow rate (AR) [m3/h] or reynolds number (Re) [-])
환기캡 형상과 정압 손실 및 손실계수 KL의 상관관계 분석
IBM SPSS Statistics 25를 이용하여 정압 손실과 손실계수 KL 를 각 변수(Cap of Adverse wind Prevention의 유무, 풍속, 유량, Cap Volume, Cap Neck Area, Cap Net Area, Cap Open Area, Reynolds number)간 이변량 상관분석을 실시하였다.
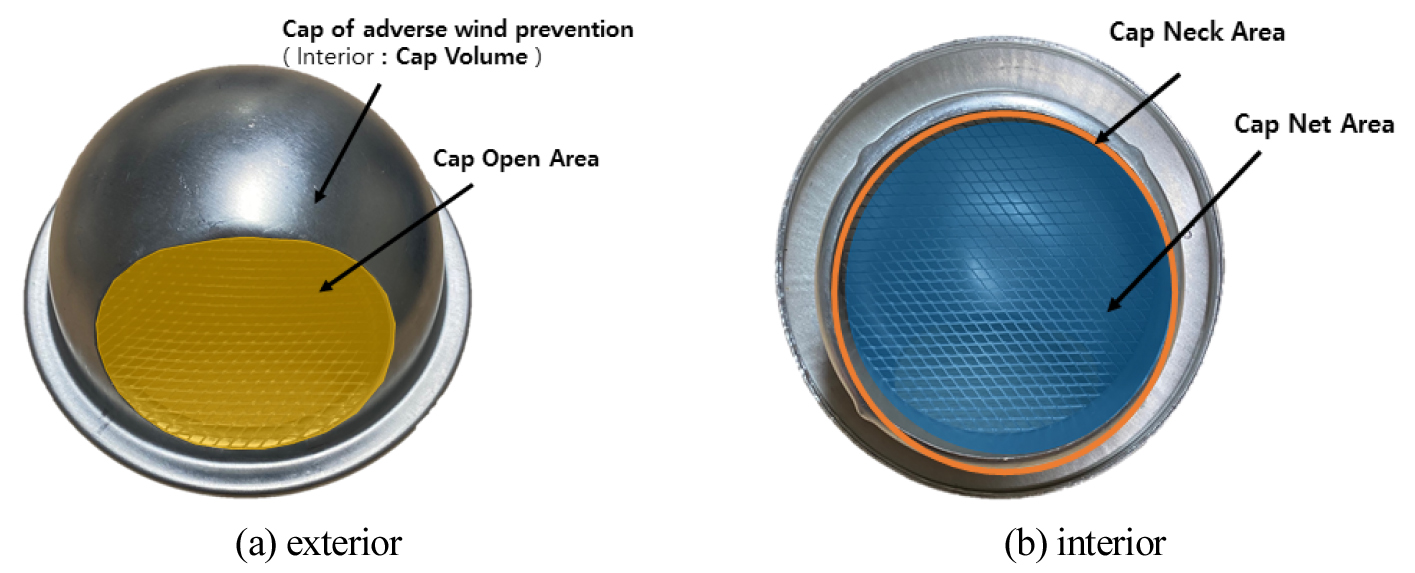
Figure 3은 상관분석을 위한 환기캡 영역을 정의한 것이다. 국내에서 가장 많이 사용되는 환기캡 No. 1을 예로 들어 설명하였다. Figure 3에 a)는 환기캡 No. 1의 외부모습을 나타내었다. 노란색으로 표시된 영역은 환기캡의 배출 공기와 외부 공기가 만나는 면적으로 Cap Open Area로 지칭하였다. 역풍 방지형 캡의 유무를 Cap of adverse wind prevention(이하 C.A.P)으로 지칭하며 정압 손실 및 손실계수 KL와의 상관관계를 분석하였다. 캡 내부 벌레 유입 방지 망에서부터 역풍 방지형 캡 사이 공간의 부피를 Cap Volume으로 지칭하였다. Figure 3에 b)는 환기캡 No. 1의 내부 모습을 나타내었다. 주황색 원으로 표시된 면적은 덕트에 맞물리는 환기캡의 면적으로 Cap Neck Area로 지칭하였다. 파란색으로 표기된 영역은 환기캡 내부에 설치되어 있는 벌레 유입 방지망의 면적을 나타내며 Cap Net Area로 지칭하였다.
Table 4는 상관분석의 결과를 나타내었다. 상관분석은 총 8가지의 변수로 분석하였으며, C.A.P은 역풍 방지용 캡의 유무를 나타내어 환기캡 No. 7과 환기캡 No. 8은 역풍 방지용 캡이 없는 0의 값으로, 그 외 환기캡은 1의 값으로 분석하였다. Static Pressure Loss값은 S1, S2, S3에서 측정된 정압 손실의 평균값을 이용하였다. 정압 손실과 음의 상관을 나타내는 변수는 C.A.P, Cap Volume, Cap Net Area, Cap Open Area였고, 그 외는 양의 상관을 나타내었다.
Table 4.
Correlation analysis result about static pressure loss and pressure loss coefficient
| C.A.P. | S.P. | V. | A.R. | P.C. | C.V. | C.N.A. | C.Net.A. | C.O.A. | Re. | |
| S.P. | -0.593** | 1 | 0.194 | 0.194 | 0.612** | -0.492** | 0.030 | -0.275 | -0.603** | 0.194 |
| sig. | 0.000 | - | 0.288 | 0.288 | 0.000 | 0.004 | 0.871 | 0.128 | 0.000 | 0.288 |
| P.C, | -0.762** | 0.612** | -0.375* | -0.375* | 1 | -0.453** | -0.294 | -0.612** | -0.603** | -0.376* |
| sig. | 0.000 | 0.000 | 0.035 | 0.034 | - | 0.009 | 0.102 | 0.000 | 0.000 | 0.034 |
여기서 유의 확률이 0.05이하인 상관관계가 높은 변수는 C.A.P, Pressure loss Coefficient, Cap Volume, Cap Open Area이다. 손실계수 KL와 양의 상관을 나타내는 변수는 Static Pressure loss가 있고, 그 외는 음의 상관을 나타내었다. 여기서 상관관계가 높은 변수는 C.A.P, Static Pressure loss, Cap Net Area, Cap Open Area로 평가되었다.
CFD의 물리적 재현성 및 신뢰도 확인
CFD 해석 개요
본 연구의 시뮬레이션은 ANSYS FLUENT 2020 R1을 이용하여 해석하였다. CFD의 물리적 재현성과 신뢰도 확인을 위해 앞서 진행된 실험을 기반으로 해석하였다. 시뮬레이션은 국내에서 주로 사용되고 있는 환기캡 No. 1과 환기캡 No. 3을 바탕으로 해석하였다(강경모 외, 2017).
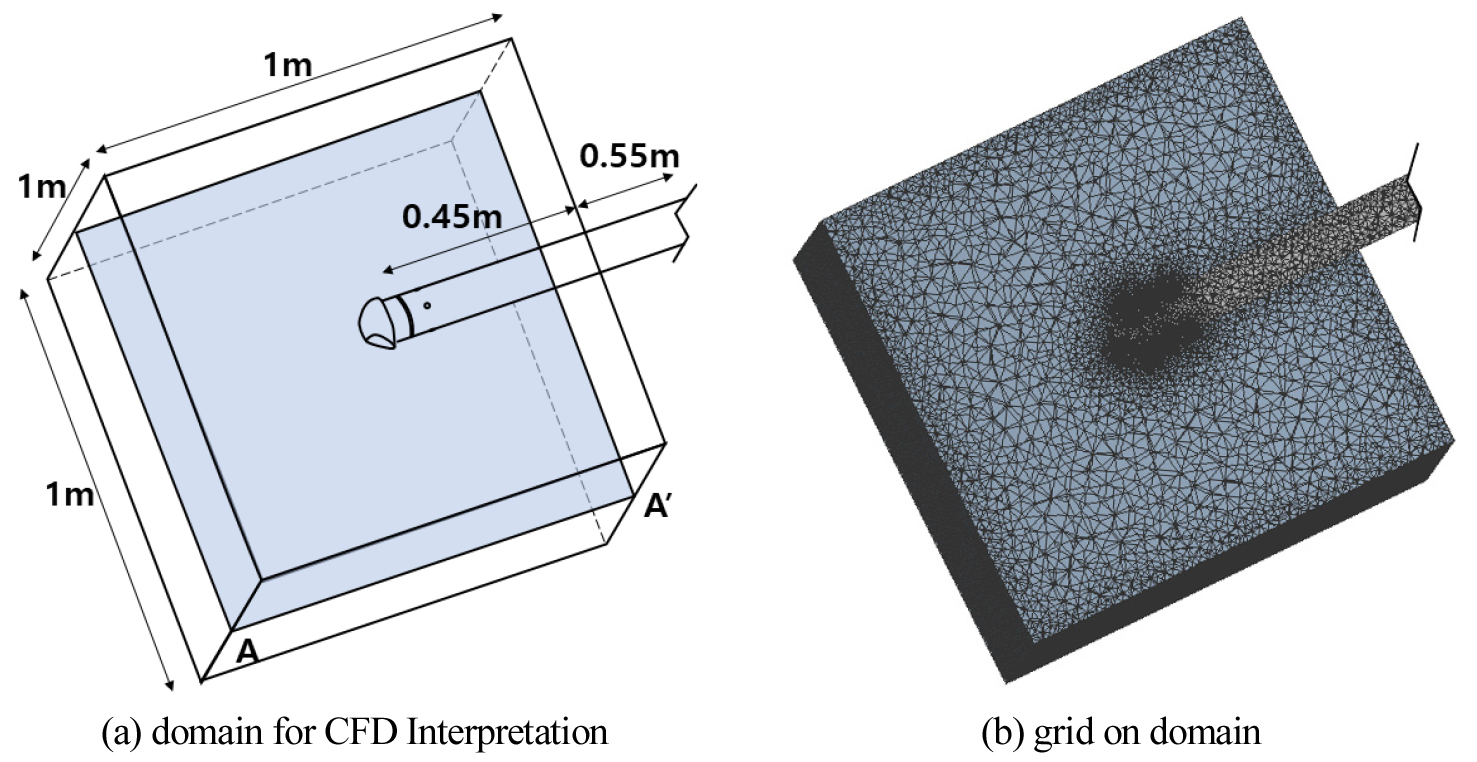
Figure 4는 해석 대상의 공간과 격자의 구성을 나타낸다. 격자의 생성 결과와 해석 결과를 보기 위한 단면은 환기캡을 중심으로 수직 단면 A-A’로 나타내었다. 기류의 안정을 위해 환기캡에 도달하기까지의 덕트 길이는 1 m로 하였다. 해석 대상은 폭, 길이, 높이가 각각 1 m인 공간을 구성하였으며, 환기캡의 형상은 실제와 유사하게 모델링 하였다. 압력은 실험과 동일하게 환기캡으로부터 0.1 m 떨어진 위치에 상측, 하측, 우측에 압력센서 크기의 면에서 해석하였다. 환기캡 형상이 복잡하기 때문에 CFD의 물리적 재현성은 격자에 대한 의존성이 가장 클 것으로 판단하였다. 환기캡 형상에서 좁은 면적과 edge 부분은 격자를 세밀화하였다. 해석영역의 격자 개수는 약 130만개이다.
덕트의 입구를 Velocity inlet, 환기캡의 출구를 Interior outlet, 외부 영역을 Pressure outlet으로 설정하였다. Velocity Inlet은 환기캡 No. 1에서 풍속 6.10 m/s, 4.10 m/s, 1.97 m/s로 해석하였으며 환기캡 No. 3는 풍속 6.08 m/s, 4.08 m/s, 2.03 m/s로 실험에서 측정된 실측치를 경계조건으로 해석하였다. 실험 시 측정한 실험체 온도를 해석 조건으로 이용하였다. 난류 모델은 복잡한 구조의 평균 유동해석에 탁월한 능력이 있고 유체 유동 해석에 가장 범용적으로 사용되고 있는 Realizable k-epsilon을 사용하였다(Mikhail and Panel, 2013; Liu et al., 2013; 권혁민과 양정훈, 2017).
CFD 해석 결과
실험과 CFD 해석의 재현성과 신뢰도를 확인하기 위해서 실험과 같은 물리적 조건을 고려하였다. 환기캡 No. 1과 환기캡 No. 3은 3가지의 풍속을 적용하였으며, 3개 위치에서의 압력을 평균하여 실험값과 비교하였다.
Figure 5는 풍속이 약 6 m/s일 때 환기캡별 풍속 분포 결과이다. 앞서 실험에서 환기캡 No.1은 풍속이 6.10 m/s, 4.10 m/s, 1.97 m/s일 때 압력을 측정하였다. 각 풍속에서 실험값은 131.67 Pa, 59.1 Pa, 12.57 Pa이고 해석 값은 133.34 Pa, 59.99 Pa, 13.85 Pa이였다. 따라서 환기캡 No. 1에서의 오차는 1.3~10.2% 범위 내에 있었다. 환기캡 No. 3는 풍속이 6.08 m/s, 4.08 m/s, 2.03 m/s일 때 압력을 측정하였다. 각 풍속에서 실험값은 162.33 Pa, 73.97 Pa, 18.20 Pa이고 해석값은 143.32 Pa, 64.71 Pa, 15.72 Pa이였다. 여기서 환기캡 No. 3에서 오차는 11.7~13.6% 범위 내에 있었다. 오차의 범위가 10% 내외이므로 해석 모델은 신뢰성이 있다고 판단하였다.
CFD를 이용한 환기캡 직경에 따른 정압 손실 해석
CFD 해석 개요
주방 후드나 욕실 환기팬의 직배기 계통에서 주로 사용되는 환기캡의 직경은 100 mm이다. 풍량에 따라 덕트의 직경이 달라지는 전열교환기의 경우 125 mm, 150 mm 등 다양한 직경의 환기캡을 사용한다. 실험을 통해 직경 100 mm의 환기캡을 이용하여 풍속과 정압 손실을 측정하였고, CFD 해석으로 재현성과 신뢰성을 파악하였다. 실험에서 재현하지 못한 다양한 직경의 환기캡에서 정압 손실과 손실계수를 해석하기 위해 신뢰도를 확인한 realizable k-epsilon 모델로 해석하였다. 직경 75 mm, 125 mm, 150 mm, 200 mm의 환기캡 No. 1과 환기캡 No. 3을 실제 형상과 유사하게 모델링 하였다. 해석영역은 Figure 4와 동일하며 환기캡과 덕트의 직경만 변경하였다. 압력은 실험과 같이 덕트의 상, 하, 우측에 직경 10 mm의 면에서 측정했으며, Velocity inlet 은 2~10 m/s내에서 2 m/s씩 풍속을 감소시키며 해석하였다. 해석은 등온 조건으로 하였으며, 해석 영역의 격자 개수는 약 250만~400만개이다.
CFD해석 결과
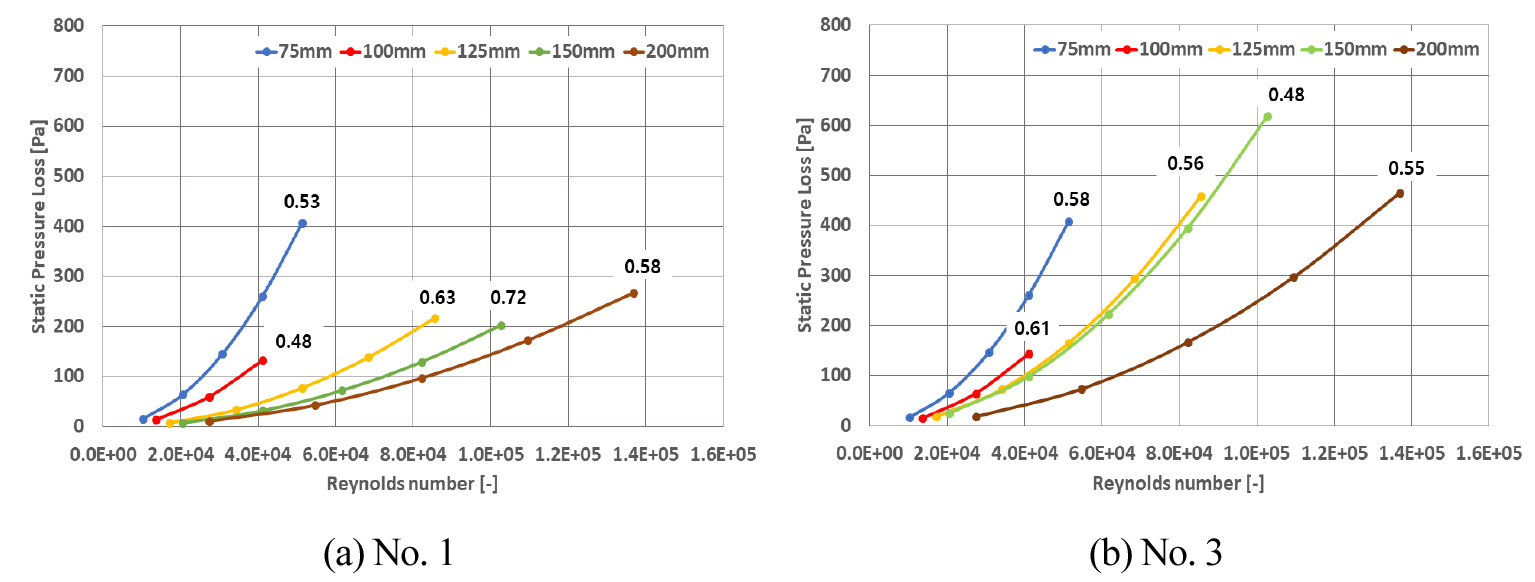
환기캡 No. 1과 환기캡 No. 3의 직경을 75 mm, 125 mm, 150 mm, 200 mm로 변화시키며 CFD 해석을 이용하여 정압 손실을 도출하였다. Figure 6은 해석된 환기캡의 정압 손실과 레이놀즈수의 관계를 나타내는 그래프다.
직경 100 mm의 결과는 CFD 물리적 재현성 및 신뢰도 확인 결과를 사용하였다. 그래프에 적힌 숫자는 덕트 단면적(A) 대비 환기캡 개방 면적(Ao)의 값이며 이후 Ao/A로 칭하였다. 실제 환기캡의 실측사이즈로 모델링하여 개방 면적을 산출하였다. 실제 환기캡 제작 과정에서 직경 변화 시 알 수 없는 이유로 Ao/A는 규칙성이 없는 것을 볼 수 있었다. 직경이 75 mm인 두 환기캡은 Ao/A와 정압 손실이 유사하였다. 직경 125 mm와 직경 150 mm의 환기캡 No. 3는 환기캡 No. 1보다 Ao/A가 작으며 정압 손실이 컸다. 따라서 환기캡의 형상이 정압 손실에 큰 영향을 미치는 것을 알 수 있었다.
물리적으로 Euler 수를 의미하는 손실계수 KL를 식 (2)를 이용하여 산출하였다(Cortes and Gil, 2007; Zhao, 2009). 환기캡 No. 1의 손실계수는 직경 75 mm에서 6.71±0.06, 직경 125 mm에서 3.58±0.03, 직경 150 mm에서 3.32±0.05 그리고 직경 200 mm에서 4.47± 0.03으로 산출되었다. 환기캡 No. 3의 손실계수는 직경 75 mm에서 6.79±0.003, 직경 125 mm에서 7.65±0.02, 직경 150 mm에서 10.23±0.06 그리고 직경 200 mm에서 7.65±0.11로 산출되었다. 직경 75 mm일 때 두 환기캡의 손실계수가 더 큰 것을 알 수 있었다. 두 환기캡에서 직경별 유량 및 레이놀즈수에 따른 정압 손실 회귀방정식을 Table 5에 제시하였다. 회귀식은 풍속 2~10 m/s 내에서 유효하다. 모든 Case에서 회귀식의 결정 계수 R2은 1.00이다.
Table 5.
Static pressure loss regression equation according to airflow rate and reynolds number by diameter of ventilation cap models (y : static pressure loss (Pa), x : airflow rate (AR) [m3/h] or reynolds number (Re) [-])
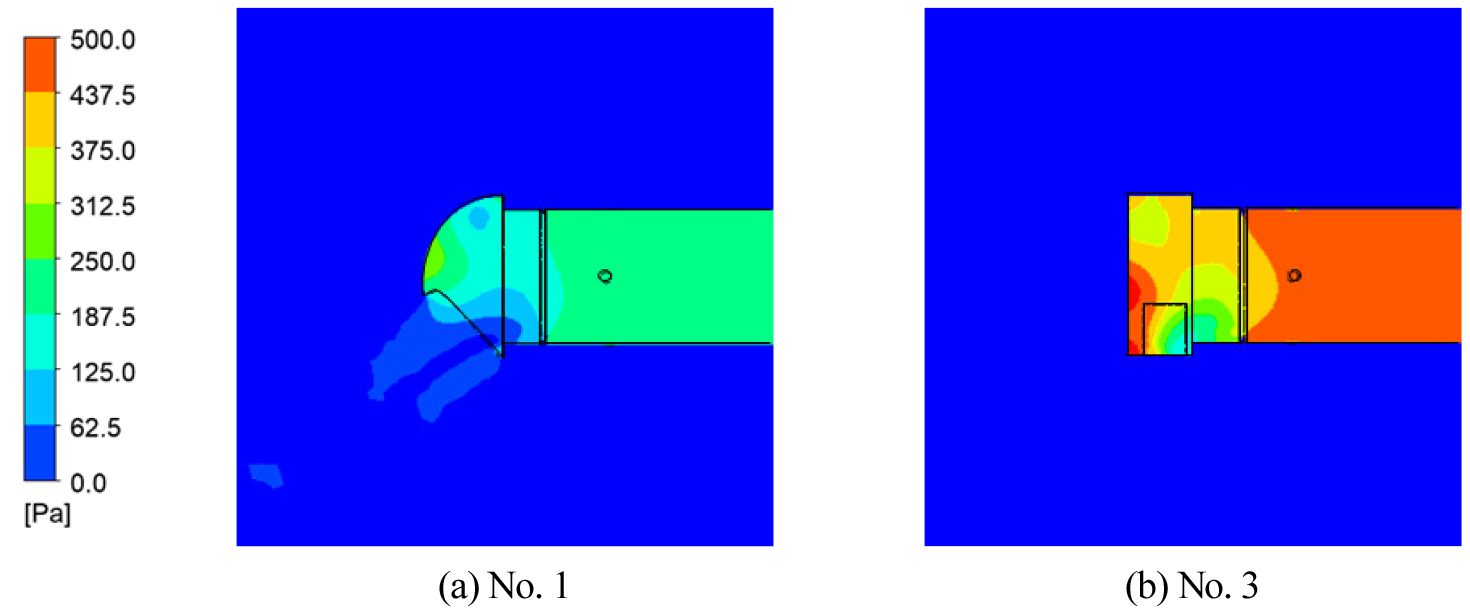
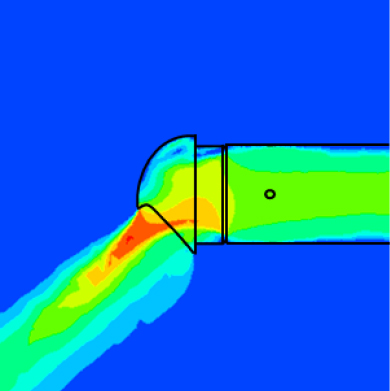
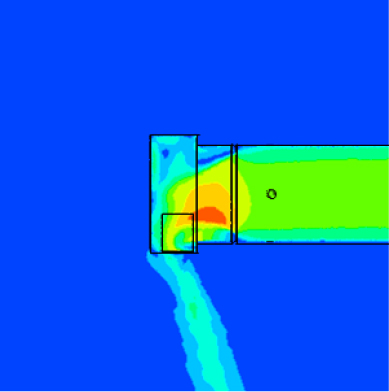
“신축 공동주택 등의 기계환기설비의 설치 기준”에 의해 설치되는 전열교환기는 급기와 배기 덕트의 직경으로 125 mm를 많이 사용한다. Figure 7은 직경 125 mm의 환기캡에 풍속이 10 m/s 일 때 압력 분포를 나타내었다. 환기캡 No. 3의 경우 환기캡의 역풍 방지 부분에서 기류가 부딪혀 정압 손실이 발생하는 것을 볼 수 있었다. 두 환기캡의 상부에는 기류가 닿지 않아 비교적 낮은 정압 손실을 나타내었다. 또한 직경 125 mm의 Ao/A는 환기캡 No. 1에서 0.63, 환기캡 No. 3에서 0.56으로 환기캡 No. 1의 개방면적 비율이 더 크다. 그로 인하여 환기캡 No. 1의 정압 손실은 환기캡 No. 3의 정압 손실보다 작았다.
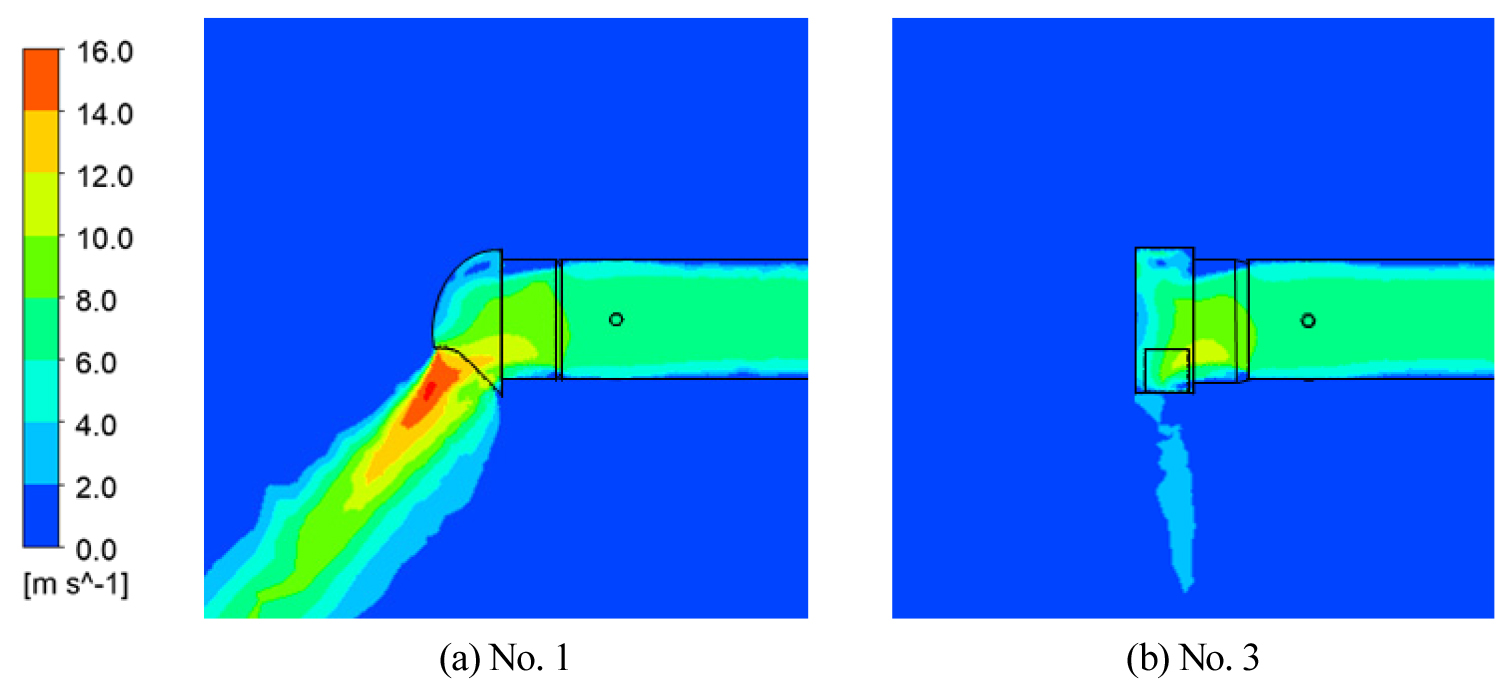
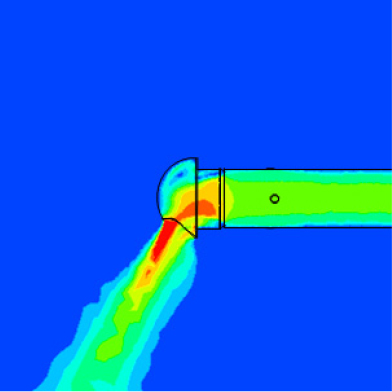
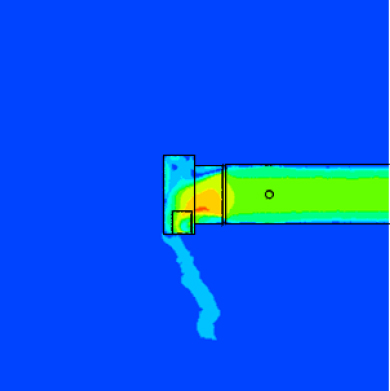
Table 6은 풍속이 10 m/s일 때 직경별 환기캡의 속도 분포를 나타내었다. 직경 150 mm, 200 mm의 결과 사진은 생략하나, 정압 손실이 더 적은 환기캡 No. 1에서의 풍속이 더 큰 것을 볼 수 있었다. 또한 환기캡 No. 1은 환기캡 개방면 방향으로 기류가 분포되고, 직경이 커질수록 기류 방향의 각도가 커졌다. 환기캡 No. 3은 역풍 방지 부분에 기류가 부딪혀 뒤쪽으로 흘러가는 것을 볼 수 있었으며, 직경이 커질수록 기류가 환기캡 개방면 방향으로 변화되었다.
결 론
이 연구에서는 직배기 시스템에서 건물의 외벽에 설치되는 환기캡의 형상이 정압 손실 및 기류특성에 미치는 영향을 알아보고 P-Q곡선과 P-Re곡선 등의 정보를 제공하기 위해 실험과 CFD 시뮬레이션 해석을 실시하였다. 연구의 주요 결과는 다음과 같다.
(1)환기캡의 형상에 따라 재현되는 최대 풍속이 달랐으며, 풍속이 2 m/s일 때 환기캡 No. 7에서 251 Pa로 가장 큰 정압손실이 발생하였고, 환기캡 No. 2에서 3.8 Pa로 가장 작은 정압손실이 발생하였다.
(2)이변량 상관분석을 통해 정압손실과 음의 상관을 나타내는 변수는 Cap of Adverse wind Prevention의 유무, Cap Volume, Cap Net Area, Cap Open Area였고, 풍속, 유량, Cap Neck Area, 레이놀즈수는 양의 상관을 나타내었다. 여기서 유의확률이 0.05 이하인 변수는 Cap of Adverse wind Prevention의 유무, Cap Volume, Cap Open Area로 나타났다.
(3)덕트의 단면적 대비 환기캡의 개방면적(Ao/A)이 정압손실과 반비례하여 영향을 주는 것을 알 수 있었다.
(4)환기캡 No. 1은 환기캡 개방면 방향으로 기류가 분포되고, 직경이 커질수록 기류의 각도가 커졌다. 환기캡 No. 3은 역풍 방지 부분에 기류가 부딪혀 뒤쪽으로 흘러가는 것을 볼 수 있었으며, 직경이 커질수록 기류가 환기캡 개방면 방향으로 변화되었다.
본 연구는 환기캡의 정압 손실에 대한 연구로 외부풍의 풍속프로파일 및 풍향에 따른 영향은 고려되지 않았다. 향후 연구에서는 환기캡의 교차오염에 대하여 외부풍의 풍속프로파일과 풍향의 영향을 검토할 예정이다.